Изучение эффекта Джоуля-Томсона (Лабораторная работа № 2), страница 2

          Сумма  называется энтальпией системы. Это ещё одна функция состояния, то есть функция, изменение которой не зависит от процесса, а определяется только начальным и конечным состоянием газа. Напомним, что к функциям состояния относятся также, например, такие параметры как объём, давление, энергия, энтропия газа.

          Итак, мы пришли к выводу, что в процессе Джоуля-Томсона энтальпия газа не меняется, то есть процесс изоэнтальпный.

                    и        ,                          (3.8)

          Будем рассматривать процесс при малых перепадах давления  и при малых, соответственно, изменениях температуры газа . Такой процесс называют дифференциальным процессом Джоуля-Томсона, в отличие от интегрального процесса, где перепады давления могут составлять десятки и даже сотни атмосфер.

          В случае дифференциального процесса, нулевое изменение энтальпии можно записать так:

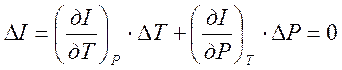,                               (3.9)

          Учитывая, что , а , находим коэффициент Джоуля-Томсона, представляющий собой отношение изменения температуры  к перепаду давления на пробке .

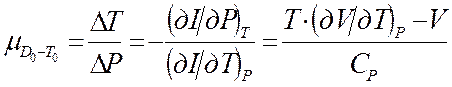.                (3.10)

          Воспользовавшись уравнением (3.10), вычислим коэффициент Джоуля-Томсона для идеального газа. В этом случае:

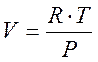       и       .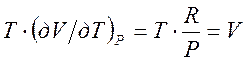

          Подставляя этот результат в (3.10), находим, что для идеального газа коэффициент Джоуля-Томсона . Это значит, что при расширении идеального газа в процессе Джоуля-Томсона, его температура остаётся постоянной, то есть температурный перепад .

          Теперь рассмотрим поведение реального газа в процессе Джоуля-Томсона. Общая термодинамическая теория эффекта остаётся прежней, но для получения из неё конкретных результатов, воспользуемся на этот раз термическим уравнением состояния реальных газов Ван-дер-Ваальса:

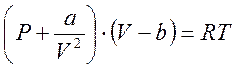.                                              (3.11)

для расчёта коэффициента Джоуля-Томсона  необходимо знать производную  (см. 3.10). Для её отыскания продифференцируем (3.11) по T, считая давление P постоянным:

.

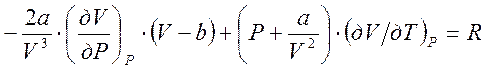Отсюда следует, что:

.

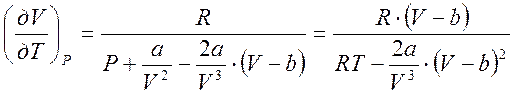          Упростим задачу, ограничившись рассмотрением разрежённого реального газа. В этом случае слагаемые, содержащие постоянные a и b, являются малыми поправками. В связи с этим можно пренебречь всеми членами с высшими степенями aи b. В этом приближении:

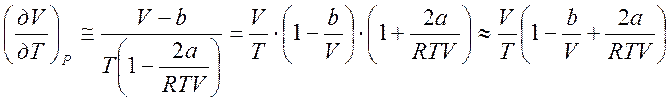,          (3.12)

          Используя последний результат в формуле (3.10), получим выражение коэффициента Джоуля-Томсона для разрежённых газов:

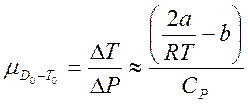.                                   (3.13)

          Таким образом, дифференциальный эффект Джоуля-Томсона для реальных газов зависит от поправок a и bв уравнение Ван-дер-Ваальса, причём они доказывают противоположное влияние на знак эффекта.

          Если 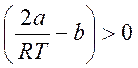, то  и газ при протекании через пробку охлаждается. (Здесь уместно напомнить, что в процессе Джоуля-Томсона ). Этот эффект называется положительным.

          Эффект отрицателен, когда 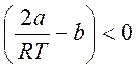 и, соответственно, 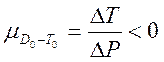. При отрицательном эффекте температура газа в процессе Джоуля-Томсона увеличивается. Легко видеть, что при  и  газ всегда охлаждается, а при  и  - всегда нагревается. Если присутствуют обе поправки, то можно указать температуру газа, когда эффект отсутствует:

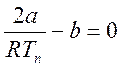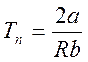;                                        (3.14)

          Эта рубежная температура  называется температурой инверсии. При такой температуре газа эффект Джоуля-Томсона отсутствует, . При температуре газа, выше температуры инверсии , газ в процессе Джоуля-Томсона охлаждается, при  - нагревается.

          Для большинства газов температура инверсии значительно выше комнатной температуры, поэтому чаще в опыте Джоуля-Томсона газ охлаждается, то есть существенней оказывается влияние на эффект поправки .

          В данной работе измеряют коэффициент Джоуля-Томсона  для воздуха при комнатной температуре и оценивают значение постоянной  в уравнении Ван-дер-Ваальса (3.4).

5. Экспериментальная установка

Рабочим элементом установки является текстолитовая гильза (поз. 1), в которой находится войлочная пробка (поз. 2), образующая пористую перегородку. Воздух прокачивается сквозь перегородку при помощи компрессора (поз. 3). Избыточное давление на перегородке регулируется вентилем (поз. 4.), соединяющим линию с атмосферой. Закрывая вентиль, можно поднимать давление на перегородке от 0 до 0,6 МПа. Это избыточное давление регистрируется манометром (поз. 5). Температура воздуха перед перегородкой (поз. 6), расположенной на входе газового потока. Температурный перепад  на пористой пробке измеряется с помощью дифференциальной хромель-копелевой термопары, спаи которой расположены в потоке по обе стороны от перегородки (поз. 7).