Изучение зависимости состава пара от состава раствора, страница 4

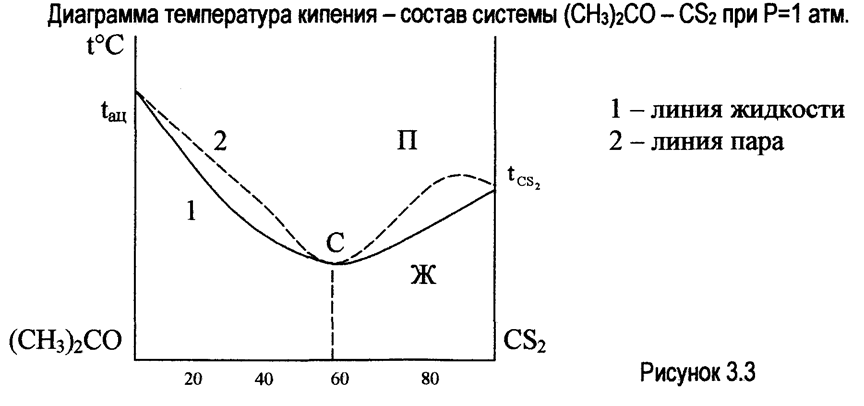
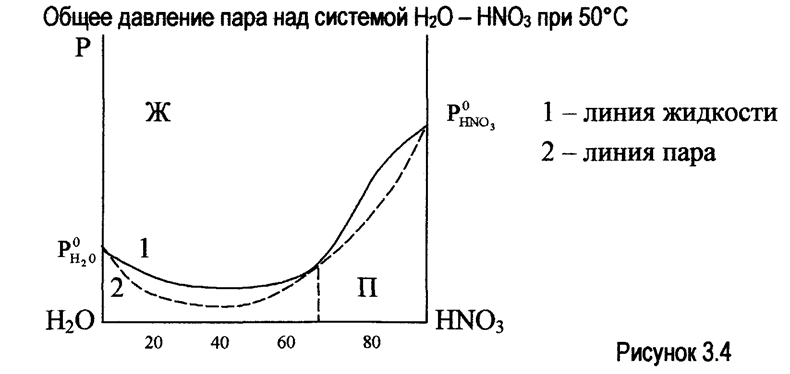
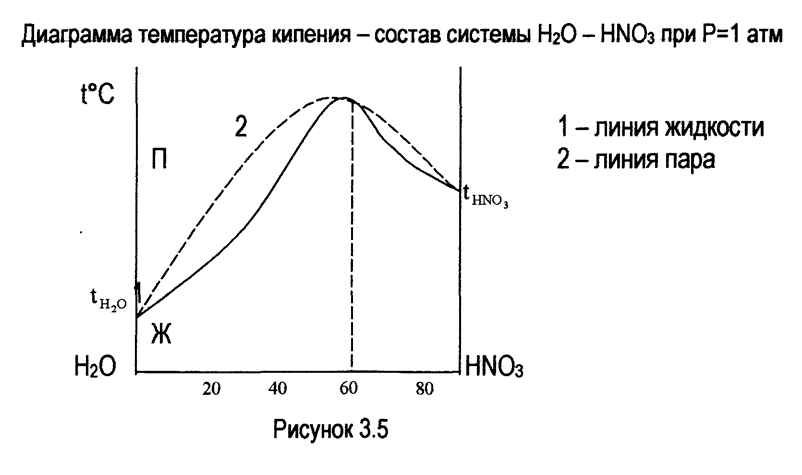
В системах, имеющих максимум, на кривых температура - состав (t° - с), дистиллят обогащается компонентом, который был в избытке по отношению к азеотропному составу (водой - при разгонке системы, содержащей от 0 до 58% НNО₃ и азотной кислой при разгонке системы, содержащей от 58 до 100% НNО₃). В перегонном кубе накапливается раствор, приближающийся по составу к азеотропному.

Применяя правило фаз к равновесию жидкость - пар при Р = const, мы видим, что число степеней свободы:

S=K-f+ l=2-2+ l=l,

то есть каждому составу фазы соответствует определённая температура кипения.

Докажем теоретически I и II законы Коновалова, для чего воспользуемся уравнением Гиобса-Дюгеля:

;        (3.1) переписав его в таком виде:

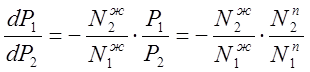                (3.2)

По закону Дальтона Р = P₁ + Р₂. Дифференцируя уравнение (3.2) по                  , получаем:

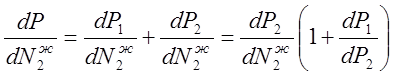                            (33)

Подставив в уравнение (3.3) значение  из уравнения (3.2), получим:

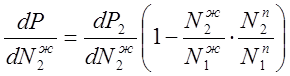                                           (34)

Проанализируем уравнение (3.4). Произво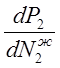дная  всегда больше нуля (по закону Рауля и Генри), оно справедливо и для неидеальных растворов, так как рост концентрации компонента в растворе обязательно приводит к увеличению его парциального давления. Если производная 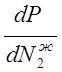>0, т.е. общее давление в системе увеличивается при добавлении к раствору второго компонента, то 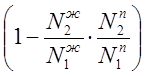>0. Это возможно только при , т.е. доказан 1 закон Коновалова.

В точках экстремумов 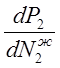 =0, поэтому уравнение (3.4) превращается в:

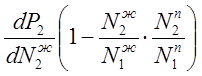                         (3.5)

 Так как 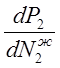 >0, то 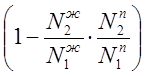=0, что возможно только при                            - одинаковых составах пара и жидкости.

3.1. Правило рычага

При помощи фазовой диаграммы можно определить количественные соотношения между фазами.

Рассмотрим изобарное нагревание жидкости в зависимости от состава (рис 3.6).

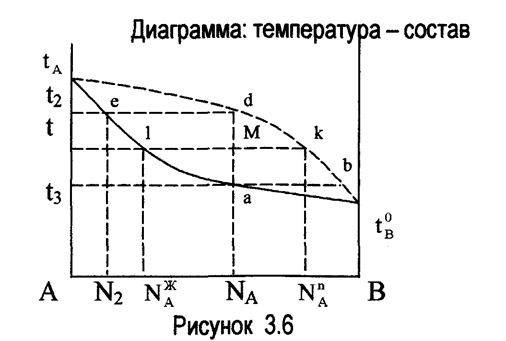
При t₁ подвод бесконечно малого количества тепла приведёт к образованию первого пузырька пара состава В. Если продолжить нагревание заключающейся жидкости, не отводя от неё пара, то постепенно выделяющиеся пузырьки пара становятся богаче менее летучим компонентом, так как новые порции пара будут выделяться из жидкости, обогащающейся компонентом А.

В момент достижения t₂ исчезает последняя капля жидкости (состава N₂). Таким образом, состав кипящей жидкости будет меняться вдоль кривой ale, состав сухого пара (насыщенного) - вдоль кривой bkd.

Если нагревание прекратить при температуре t, то первоначально гомогенная смесь окажется распавшейся на жидкость состава I () и пар состава k().          

Найдем соотношение между количеством обеих фаз. Допустим, что нагреванию подверглось g килограммов смеси. Тогда из уравнения , выражающего распределение вещества между жидкостью и паром, следует, что

    

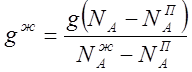
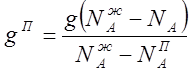
откуда:

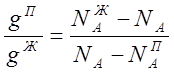
или:

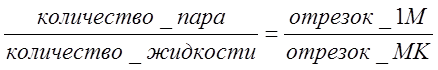
На рис 3.6 видно каким образом меняется соответствие между количеством жидкости и пара по мере нагревания (или охлаждения) в интервале t₁ - t₂.

Если представить IK в виде рычага первого рода (с точкой опоры в точке М), то рычаг будет в равновесии при условии, что массы g^п и g^ж укреплённые на концах, отвечают выведенному соотношению. Поэтому уравнение (3.6) и получило название "правило рычага".

Это правило применяется для составления материального баланса в любой гетерогенной системе, в том числе и однокомпонентной.