ЭМП системы из двух элементарных электрических вибраторов

МИНИСТЕРСТВО  ОБРАЗОВАНИЯ  И  НАУКИ  РФ

ФЕДЕРАЛЬНОЕ  АГЕНСТВО  ПО  ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТАГАНРОГСКИЙ  ГОСУДАРСТВЕННЫЙ  УНИВЕРСИТЕТ

__________________________________________________________

Кафедра Аи РПУ

РТФ

Курсовая  работа

«ЭМП системы двух ЭЭВ»

Выполнила: студентка гр.Р-73

                    Колыхан Н.В.

        Проверил: профессор кафедры

                     А и РПУ

                     Юханов Ю.В.

Таганрог 2005 г.

1.Техническое задание №24

1. Рассчитать и построить структуру силовых линий ЭМП системы из двух элементарных электрических вибраторов, расположенных на расстоянии

2. Форма тока

3. Интервал расстояний

4. Параметры среды

2.1.Постановка задачи:

Рассмотрим элементарный электрический вибратор - прямолинейная нить тока, длина которой намного меньше длины волны возбуждаемого поля, а модуль и фаза плотности линейного электрического поля распределены по длине вибратора равномерно (Рис.1)

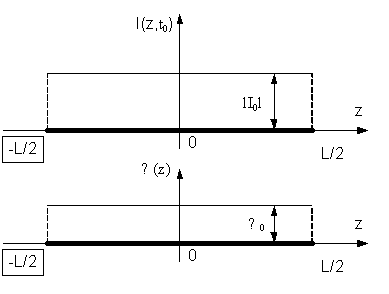
Рис.1

Элементарный электрический вибратор является математической моделью  диполя Герца, представляющего собой два металлических шара, соединенных тонким проводом, к разрезу провода подсоединен, например, с помощью двухпроводной линии источник Э.Д.С.(Рис.2)

Рис.2

Если напряжение в разрезе, создаваемое с помощью источника Э.Д.С., менять во времени по гармоническому закону, то заряды на шарах тоже меняются по гармоническому закону. Под воздействием стороннего источника заряженные частицы колеблются – двигаются между концами с переменной скоростью. Распределение модуля  и фазы электрического тока по длине диполя из-за малой его длины является близким к равномерному. Длина разреза .

Теперь введем декартовую систему координат и  расположим  два элементарных электрических вибратора длиной L параллельно оси в точках с центрами (Рис.3).

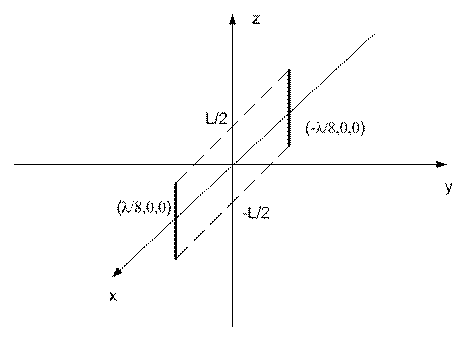
Рис.3

2.2.Решение задачи.

Так как источником магнитных потенциалов является магнитные токи, а в данном случае магнитные токи отсутствуют, то

 и .

Найдем распределение плотности электрического тока в пространстве:

      (1)

при этом токи определены на вибраторах лишь при , где L- длина вибраторов.

Поскольку токи во времени изменяются гармонически, то для решения поставленной задачи воспользуемся методом комплексных амплитуд. Найдем комплексные амплитуды токов:

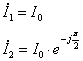
Определим векторный потенциал:

                                                                   (2)