где ![]() -точка наблюдения,
-точка наблюдения, ![]() - точка наблюдения,
- точка наблюдения, 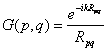 - функция Грина свободного
пространства,
- функция Грина свободного
пространства, ![]() - расстояние между точками p, q.
- расстояние между точками p, q.
![]() -коэффициент
распространения волны в данной среде, где
-коэффициент
распространения волны в данной среде, где ![]() -
-
абсолютная комплексная диэлектрическая проницаемость среды .
Подставляя (1) в (2) и применяя основное свойство ![]() -функции, получим:
-функции, получим:
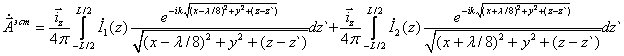 Учитываем, что распределение
тока вдоль элементарного электрического вибратора равномерно и
Учитываем, что распределение
тока вдоль элементарного электрического вибратора равномерно и ![]() ,то запишем:
,то запишем:
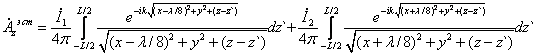 (3)
(3)
Определим вектор напряженности магнитного поля:
![]()
Тогда составляющие вектора ![]() :
:
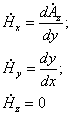
Учитывая, что ![]() , тогда при интегрировании (3)
применим теорему о среднем и получим:
, тогда при интегрировании (3)
применим теорему о среднем и получим:
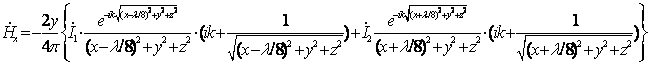
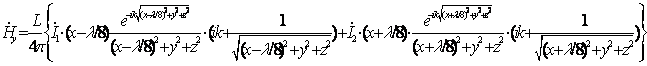 Составляющие
вектора напряженности электрического поля:
Составляющие
вектора напряженности электрического поля:
![]()
Составляющие вектора ![]() :
:
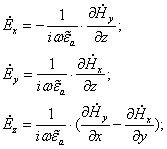
Производя дифференцирование, получим:
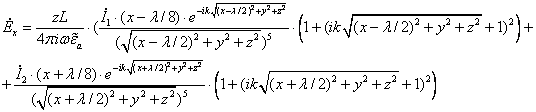
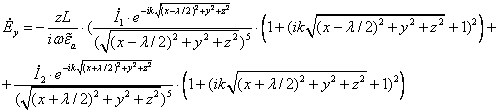
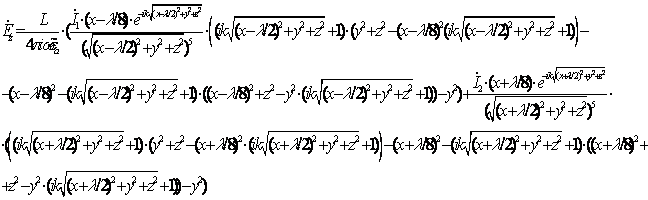 Для
нахождения зависимостей напряженностей полей от времени вычислим:
Для
нахождения зависимостей напряженностей полей от времени вычислим:
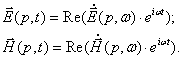
Построим силовые линии в моменты
времени t, такое, что ![]() ,
где
,
где![]() -целое число.
-целое число.
Для вектора напряженности магнитного поля:
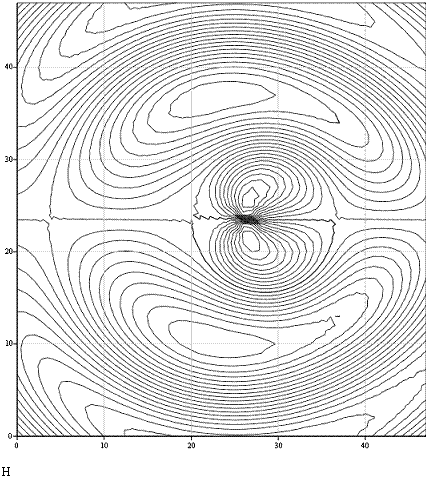
Для вектора напряженности электрического поля:
В плоскости xOy:

В плоскости zOy
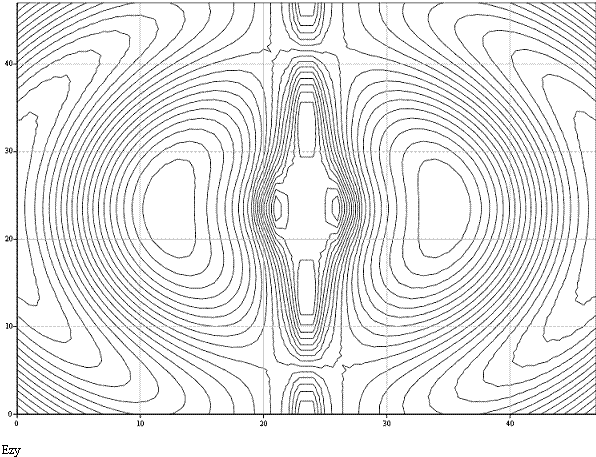
В плоскости zOx:
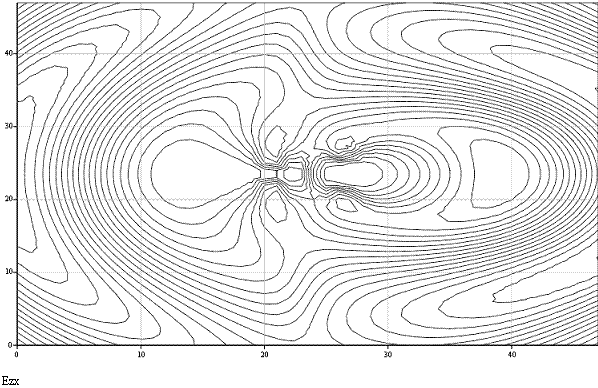
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.