Исследование закона распределения частоты отказов подвески, вызываемых износом рессор (Научно-исследовательская часть дипломного проекта)

9 Научно-исследовательская часть

9.1 Исходные данные для расчета

Исследуется закон распределения частоты отказов подвески, вызываемых износом рессор. Для установления закона распределения отказов партия подвесок, вышедших из строя, была подвергнута дефектовке и, в 82 случаях, оказалось, что причиной отказа явился повышенный износ рессор. Величина пробега подвесок с изношенными рессорами колебалась в пределах от 120 до 240 тыс. км.

Целью работы является определение величин границ нижнего и верхнего интервала оценки математического ожидания пробега шестерен с доверительной вероятностью 0,95.

В связи с этим требуется решить следующие задачи:

- построить гистограмму опытных часто по пробегу и по ее виду решить в первом приближении вопрос о законе распределения;

- для предполагаемого закона распределения построить теоретическую кривую частоты отказов по пробегу, найти основные параметры закона распределения, построить интегральную кривую;

- найти величину критерия согласия Пирсона и произвести проверку на отрицании принятого закона распределения;

- дать интервальную оценку математического ожидания;

- сделать конкретные выводы.

9.2 Расчет числовых характеристик выборки

Для удобства и наглядности расчетов приступаем к формированию таблицы 9.1, куда занесем, кроме исходных данных, значение величин, необходимых для определения параметров распределения.

Таблица 9.1 – Расчет числовых характеристик выборки

№ интервала	Границы интервалов, тыс. км	Середина интервалов, Xi, тыс. км	Опытные частоты mi	Xi×Ti, тыс. км	Xi-X, тыс. км	(Xi-X)2, тыс. км
1	120…132	126	1	126	-48,59	2361
2	132…144	138	1	138	-36,59	1338,8
3	144…156	150	4	600	-24,59	604,7
4	156…168	162	21	3402	-12,59	158,5
5	168…180	174	32	5568	-0,59	0,35
6	180…192	186	14	2604	11,41	130,2
7	192…204	198	4	792	23,41	548
8	204…216	210	3	630	35,41	1253,9
9	216…228	222	1	222	47,41	2247,7
10	228…240	234	1	234	59,41	3529,5
Σ	-	-	82	14316	-	12172,65

Параллельно заполнению таблицы ведем расчеты по определению необходимых характеристик выборки.

Среднее арифметическое значение определяется по формуле:

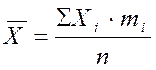                                               (9.1)

где n – объем выборки, n = 82.

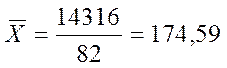 тыс. км.

Величина оценки дисперсии определяется по формуле:

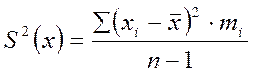                                         (9.2)

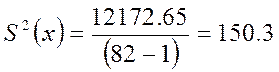 тыс. км².

Оценка среднеквадратического отклонения определяется по формуле:

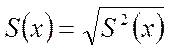                                         (9.3)

 тыс. км.

Оценка коэффициента вариации определяется по формуле:

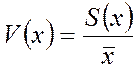                                                 (9.4)

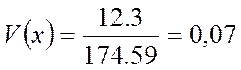
Нормальный закон распределения характеризуется плотность вероятности:

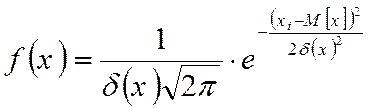                                 (9.5)

где М[х] и d(х) – соответственно математическое ожидание и среднее квадратическое отклонение случайной величины х.

Предполагаем, что теоретическое распределение является нормальным с величинами параметров М[х] =  и d(х) = S(х) заимствованными из эмпирического распределения.

9.3 Расчет теоретических кривых

Определение точек теоретических кривых удобнее проводить в табличной форме (таблица 9.2).

Таблица 9.2 – Расчет теоретических кривых