Структурный анализ систем автоматического регулирования: Методические указания к лабораторным работам по курсу "Теория автоматического управления", страница 3

2.  Необходимо произвести привязку графика ЛАЧХ к осям. Для этого необходимо выяснить, какой степенью астатизма обладает сложная передаточная функция. Тогда уравнение графика начального участка асимптотической ЛАЧХ будет иметь вид:

При наличии свободных членов  в числителе (проводится асимптота с наклоном ) —

При наличии свободных членов  в знаменателе числителе (проводится асимптота с наклоном ) –

При отсутствии свободных членов  числителе (проводится асимптота с нулевым наклоном) — .

Асимптота, описывающая начальный участок графика ЛАЧХ, должна проходить через точку с координатами , где  – наименьшая частота сопряжения.

3.  Далее график ЛАЧХ чертится от частоты к частоте сопряжения меняя наклоны. Изменение наклона графика ЛАЧХ зависит от порядка полинома и его местонахождения (числитель или знаменатель). Параметры изменения наклона приведены в таблице 1.

Таблица 1

          Для перевода произвольного полинома n – ого порядка

в произведение полиномов первого и второго порядков необходимо выполнить следующие действия:

1.  Определить корни полинома . В результате получится n корней , причём одни корни будут вещественными  а другие комплексно сопряжённые  и .

2.  Зная корни полином можно выразить в виде 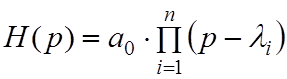 или 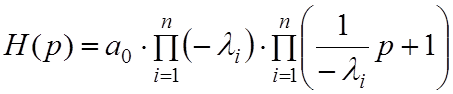. При этом 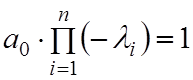. Тогда 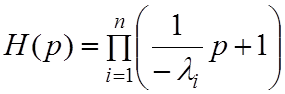. Если имеется вещественный корень , то для него будет соответствовать полином первого порядка , при этом 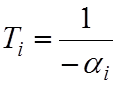. Если имеются два комплексно сопряжённых корня  и , то для них будет соответствовать полином второго порядка . При этом 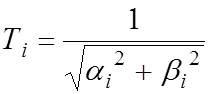 и .

ПРОГРАММА РАБОТЫ

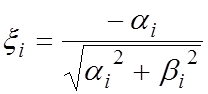1.  Изучить графики ЛАЧХ простых передаточных функций.

2.  Для заданного в таблице варианта определить передаточные функции САР по задающему и возмущающему воздействий.

3.  Определить уравнение статической характеристики для замкнутой системы и построить графики данного уравнения при  изменяя .

4.  Определить уравнение АФХ передаточной функции по задающему воздействию для замкнутой и разомкнутой систем и построить графики АФХ.

5.  Построить график ЛАЧХ и ЛФЧХ передаточной функции по задающему воздействию для замкнутой и разомкнутой систем.

6.  Начертить график асимптотической ЛАЧХ передаточной функции по задающему воздействию для замкнутой и разомкнутой систем.

7.  Проанализировать полученные результаты.

8.  Сделать выводы.

9.  Оформить отчёт по лабораторной работе.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.  По каким формулам определяются передаточные функции структуры, состоящей из звеньев с передаточными функциями W₁(p) и W₂(p), соединёнными последовательно, параллельно и в цепь с обратной связью.

2.  Запишите общую формулу для определения уравнения статической характеристики для системы с одним управляющим и одним возмущающим входом.

3.  Зарисуйте асимптотические ЛАЧХ типовых звеньев.

ВАРИАНТЫ ЗАДАНИЙ

Задана структура

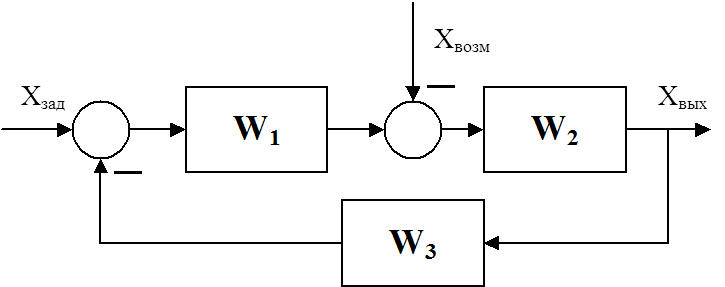
По таблице выбирается вариант

№	W1	W2	W3
1
2
3
4
5
6
7
8
9
10
11
12
13

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.  Солодовников В. В., Плотников В. Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования. Учебное пособие для вузов. – М.: Машиностроение, 1985. – 536 с.

2.  Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. Ч. 1. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др.; Под ред. А. А. Воронова. – М.: Высш. шк., 1986. – 367 с.

3.  Солодовников В. В. Основы автоматического регулирования. Т.1. —Машгиз, 1954. -- 324 с.