Структурный анализ систем автоматического регулирования: Методические указания к лабораторным работам по курсу "Теория автоматического управления", страница 2

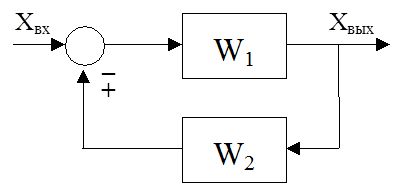
Передаточная функция системы с обратной связью равна дроби, числитель которой – передаточная функция звена прямой связи, а знаменатель – единица плюс (минус) произведение передаточных функций прямой и обратной связей ("плюс" соответствует отрицательной, "минус" – положительной обратной связи):

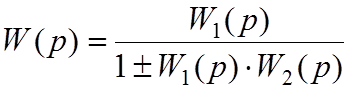
          При получении передаточных функций сложных систем с множеством звеньев и различными связями между ними основной подход к решению задачи заключается к сведению сложной структуры многоконтурной схемы к одноконтурной схеме путём замены звеньев, охваченных различными связями, укрупнёнными заменяющими звеньями, и устранению перекрёстных связей в системе. Данная задача решается с использованием правил преобразования:

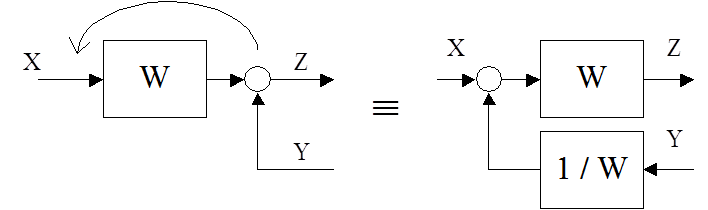
1.  Правило переноса точки съёма сигнала. Если точку съёма переносить против прохождения сигнала, то в переносимую ветвь следует включить звено  с передаточной функцией звена, находящегося на пути между новой и прежней точками съёма:

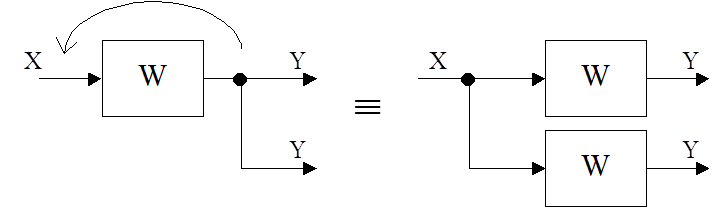
Если точку съёма переносить в направлении прохождения сигнала, то в переносимую ветвь следует включить звено с обратной передаточной функцией звена, находящегося на пути между прежней и новой точками съёма:

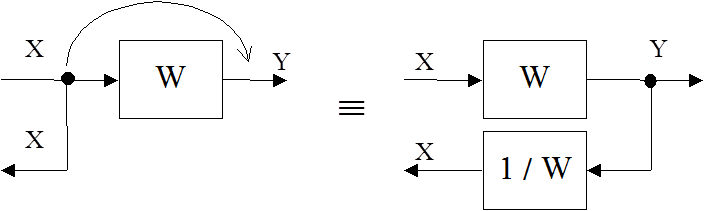
2.  Правило переноса точки суммирования сигнала. Если точку суммирования переносить против направления прохождения сигнала, то в переносимую ветвь следует включить звено с обратной передаточной функцией звена, встретившегося на пути  между новой и прежней точками суммирования:

Если точку суммирования переносить в направлении прохождения сигнала, то в переносимую ветвь следует включить звено с передаточной функцией звена, встречающегося на пути между прежней и новой точками суммирования:

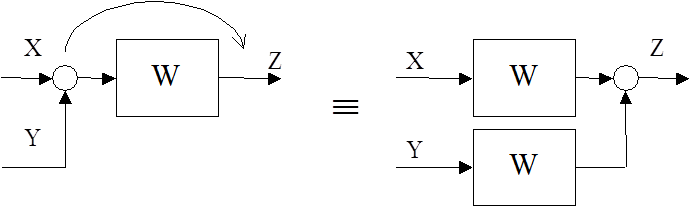
3 Статические характеристики САР

          Статические характеристики используются для отображения зависимости установившихся значений переменных САР от входных и возмущающихся сигналов. Предположим, что имеется САР с n задающими входами, m возмущающими входами и одним выходом. Тогда выражение выходного сигнала в операторной форме будет выглядеть следующим образом: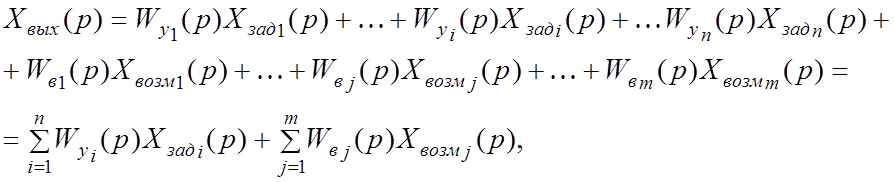

где  – передаточная функция САР по i-ому задающему входу;

 – передаточная функция САР по j-ому возмущающему входу.

Поскольку оператор р характеризует производную сигнала, а при установившемся процессе в линейных системах все производные считаются равными нулю, то оператор равен нулю и тогда передаточные функции преобразуются в некоторые постоянные величины  и :

.

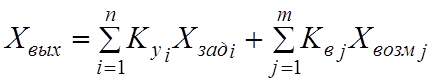Данное выражение будет представлять собой уравнение статической характеристики.

4 Частотные характеристики

          Частотные характеристики характеризуют САР по одному входу и одному выходу. Для получения частотных характеристик САР необходимо при помощи правил преобразований определить передаточную функцию САР, например по задающему входу , и произвести замену оператора р на выражение jw. В результате получим частотную передаточную функцию . Из частотной передаточной функции можно получить следующие частотные характеристики:

1.  Амплитудно-частотная характеристика (АЧХ) ,

2.  Фазо-частотная характеристика (ФЧХ) ,

3.  Логарифмическая АЧХ (ЛАЧХ) . Причём частота  также изменяется в логарифмическом масштабе.

          Для быстрого построения ЛАЧХ САР полезно уметь строить асимптотические ЛАЧХ – ЛАЧХ график, которой заменён асимптотами. Асимптотическая ЛАЧХ строится для передаточной функций числитель и знаменатель которой состоит из произведения полиномов первого и второго порядка:

, , .

В этом случае сложную передаточную функцию можно представить как произведение элементарных передаточных функций, представляющих собой каждый такой полином и коэффициента пропорциональности. Причём, полиномы, составляющие знаменатель сложной передаточной функции, будут образовывать передаточные функции:

, , .

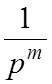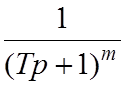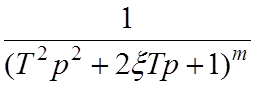          Для каждого из элементарных звеньев имеется свой известный график ЛАЧХ в асимптотическом виде. График асимптотической ЛАЧХ сложной передаточной функции образуется путём сложения асимптотических ЛАЧХ элементарных звеньев:

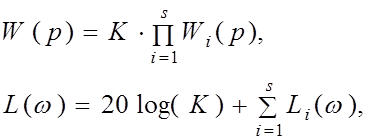
где s – количество простых полиномов в числителе и в знаменателе.

          Существует упрощённая методика построения асимптотической ЛАЧХ для любой передаточной функции:

1.  Определить частоты сопряжения для каждого полинома 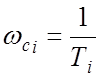, где ; Т_i – постоянная времени i – ого полинома.