Синтез систем управления технической системы. Анализ влияния параметров нелинейности на характеристики автоколебаний. Имитационное моделирование с использованием пакета Simulink, страница 2

Wkor=tf([0.25 0.25*2 0.25],[0.25 1 0])                                      перед.функция корр.звена

Transfer function:

0.25 s^2 + 0.5 s + 0.25

-----------------------

     0.25 s^2 + s

margin(Wkor)                                                            характеристика корр.звена

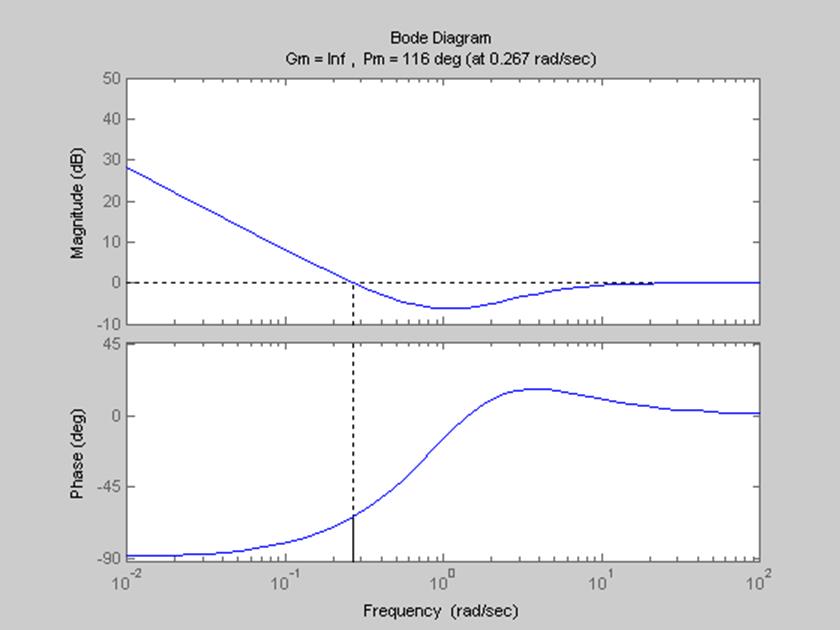
WrazGel=Wkor*Wnc1                                                               перед. функция разомк.желаемая

Transfer function:

                  1.524 s^2 + 3.048 s + 1.524

----------------------------------------------------------------

0.000625 s^6 + 0.0155 s^5 + 0.3126 s^4 + 1.255 s^3 + 1.1 s^2 + s

 margin(WrazGel)                                                                      ЛАЧХжелаемая

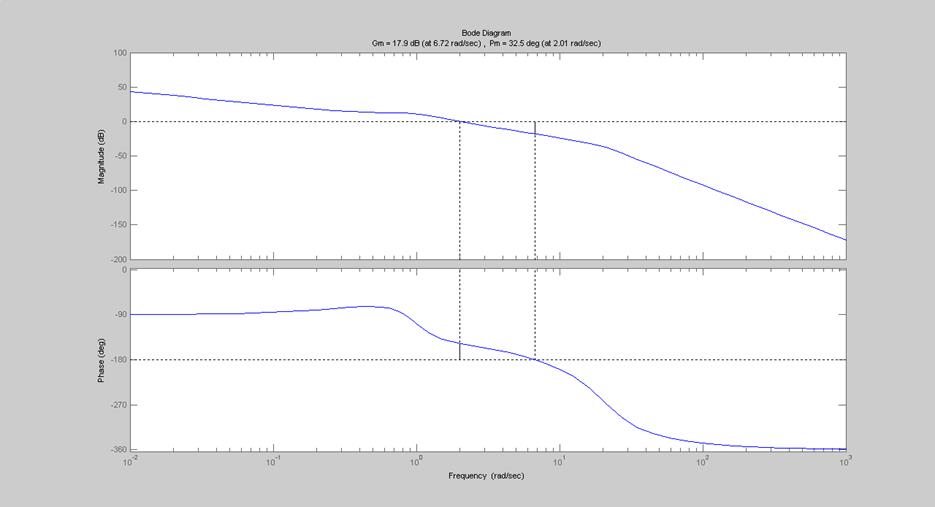
Ltiview

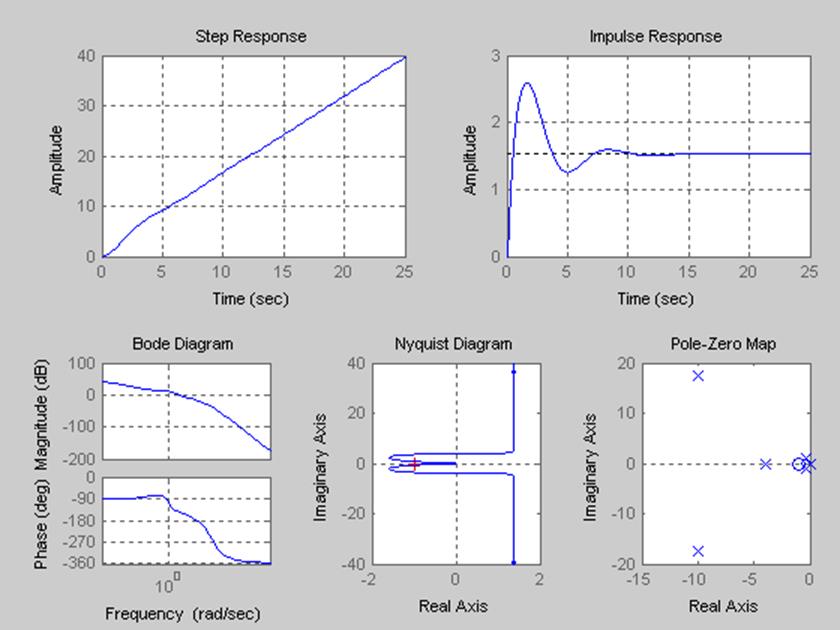
ЛАЧХ(W_нч,W_жел,W_кор)

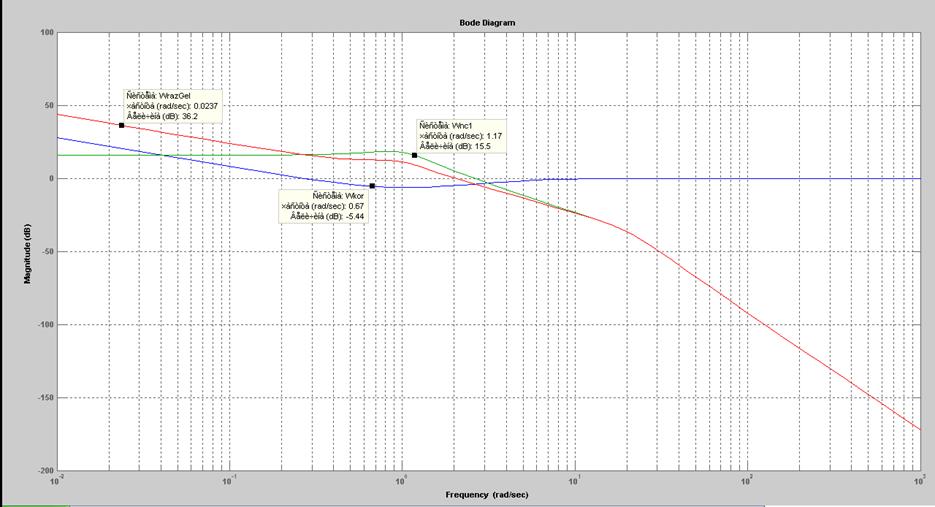
Сравнительная таблица характеристик

Тип системы	Запас по амплитуде	Запас по фазе
Wраз без коррекции	8,04 dB	12,3 deg
Wраз с коррекцией	17,9 dB	32,5 deg

Исследование замкнутых систем

Замкнутая система без корректирующего звена

Wzam=(Wpr*Wc)/(1+Wpr*Wc)

Margin(Wzam)

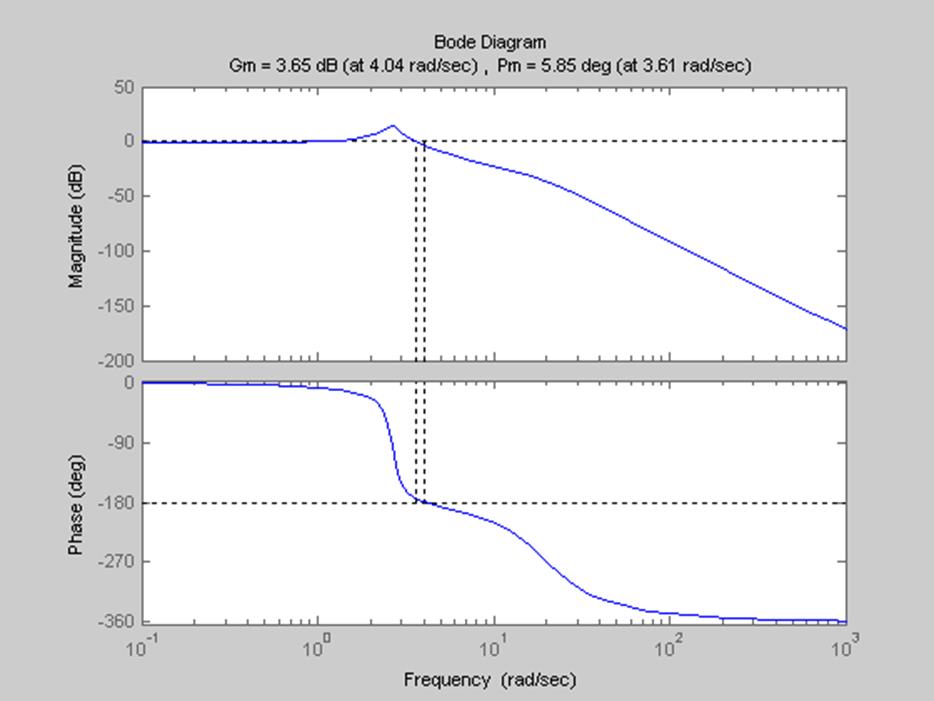
Ltiview

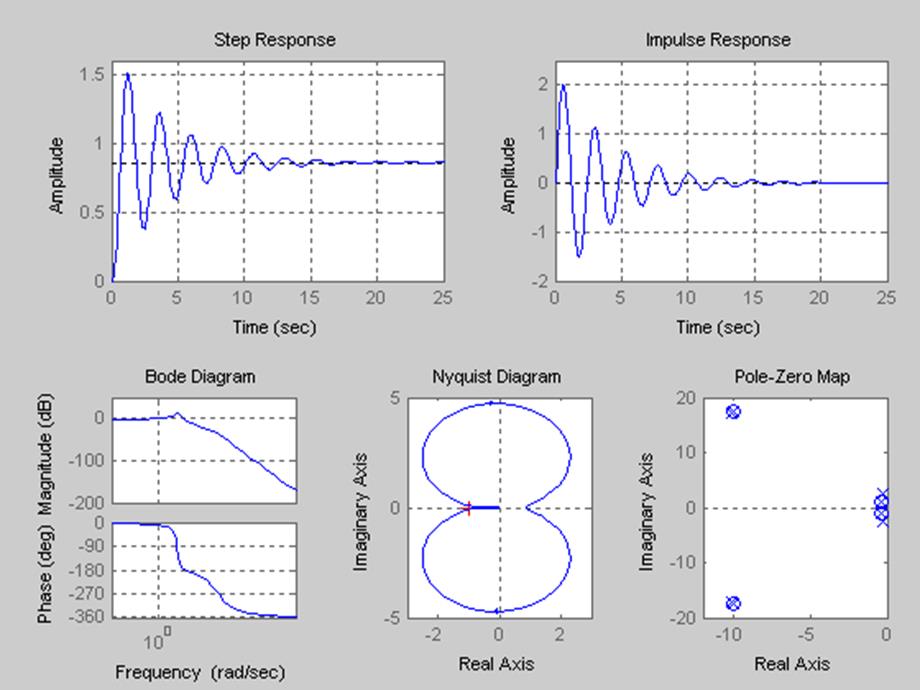
Исследование переходного процесса

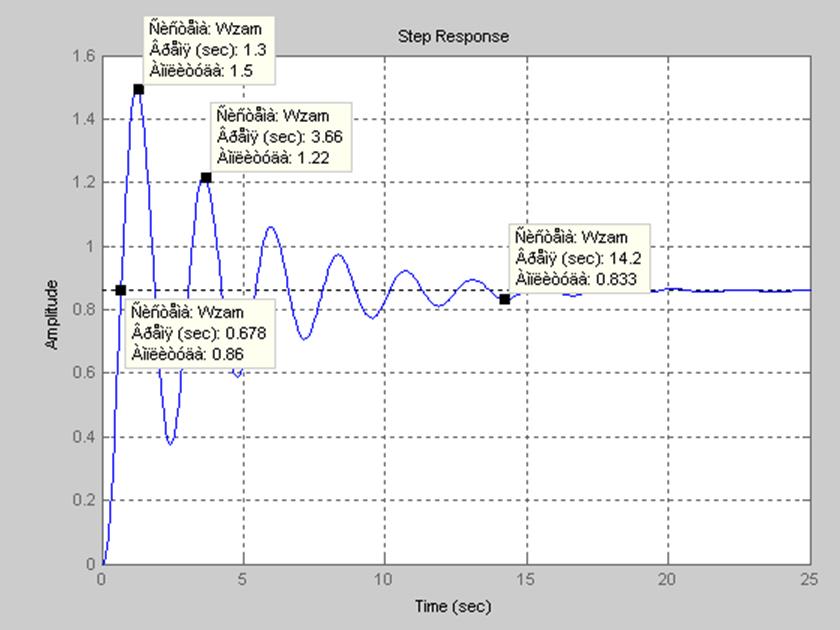
a.  время срабатывания

t_c=0,678

б.  относительное перерегулирование

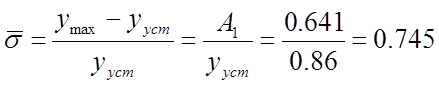
в. показатель колебательности

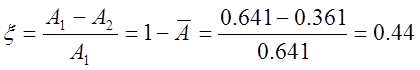
г. время регулирования

          t_p=14.2

Замкнутая система с корректирующим звеном

Wzam=(Wpr*Wc*Wkor)/(1+Wpr*Wc*Wkor)

margin(Wzam)

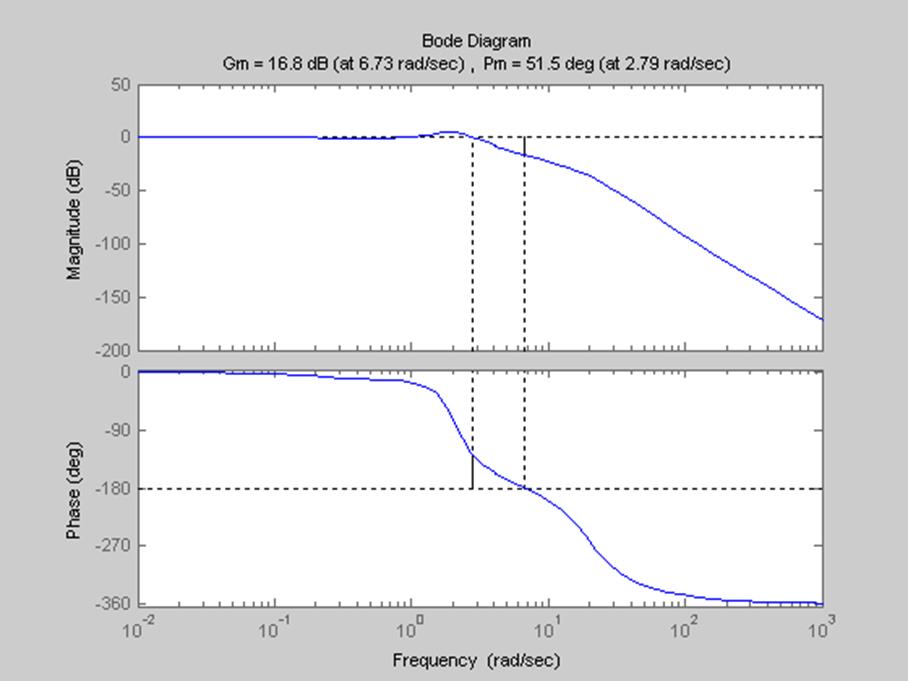
Ltiview

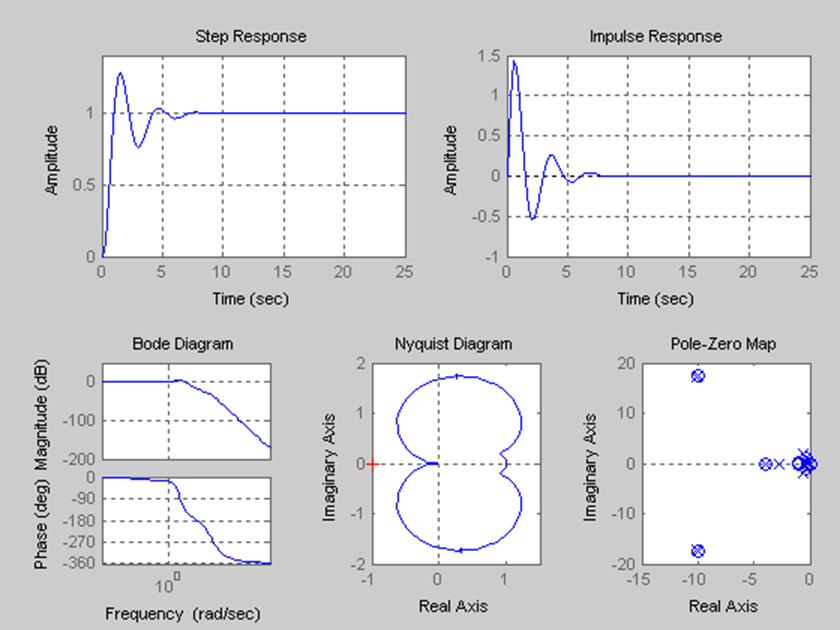
Исследование переходного процесса

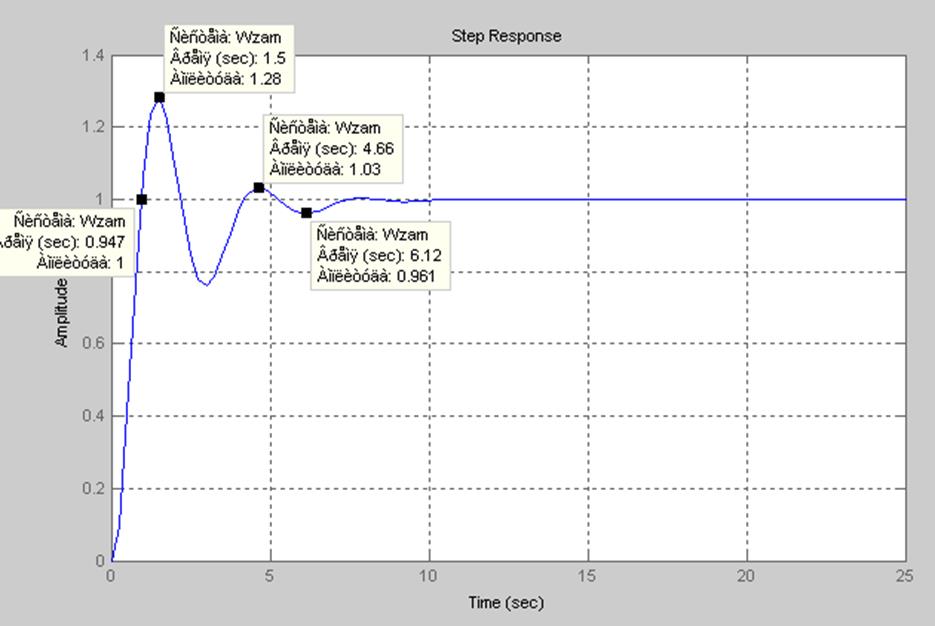
a.  время срабатывания

t_c=0,947

б.  относительное перерегулирование

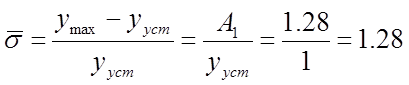
в. показатель колебательности

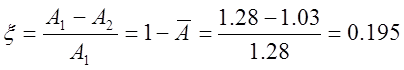
г. время регулирования

          t_p=6.12

Теоретическая часть

Определение параметров

 корректирующего звена при использовании метода последовательной коррекции.

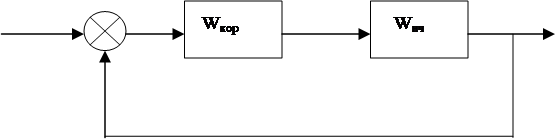При известной передаточной функции неизменяемой части системы ставится задача определить передаточную функцию последовательного корректирующего звена так, чтобы логарифмическая амплитудно-частотная характеристика разомкнутой системы была бы желаемой.

W_раз = W_жел = W_кор * W_нч

20 lg W_жел = 20 lg W_кор + 20 lg W_нч

20 lg W_кор = 20 lg W_жел - 20 lg W_нч

          Для построения желаемой логарифмической амплитудно-частотной характеристики выбирается опорная точка, в которой значение логарифмической амплитудно-частотной характеристики равно -_∆А_зап (запаса по амплитуде), что составляет от 6 до 12 дБ.

          Через опорную точку проводится желаемая логарифмическая амплитудно-частотная характеристика под углом -20 дБ/дек до пересечения с логарифмической частотной характеристикой неизменяемой части и в точке пересечения определяется частота начала коррекции.

          Амплитудно-частотные характеристики корректируются в диапазоне частот от ω₁ до ω₂, поэтому последовательно корректирующее звено рассматривается как корректирующий фильтр интервала частот от ω₁ до ω₂.

          Желаемая логарифмическая характеристика будет минимально фазовой, так как пересекает ось частот под углом -20 дБ/дек как апериодическое звено.

          Использование корректирующего звена приводит к уменьшению полосы пропускания системы и уменьшению частоты среза. Чем больше запас по амплитуде в узле коррекции ω₂, тем меньше полоса пропускания.

          Логарифмическая амплитудно-фазовая частотная характеристика корректирующего звена вычисляется по разности логарифмической амплитудно-фазовой частотной характеристики желаемой и неизменяемой части.

          Комментарий к практическому использованию метода последовательной коррекции:

1)  передаточная функция корректирующего звена определяется аналитически только на основе применения в расчетах асимптотических логарифмических амплитудно-фазовых частотных характеристик.

2)  значение запаса по фазе при выполнении расчетов не контролируются, поэтому после построения логарифмической амплитудно-фазовой частотной характеристики разомкнутой системы может потребоваться изменение интервала частот ω₂ до ω₁ в сторону увеличения, то есть надо увеличить ω₂, а ω₁ уменьшить (уменьшается полоса пропускания).

3)  если передаточная функция неизменяемой части и ее логарифмическая амплитудно-фазовая частотная характеристика определяется численно (использование оператора tf в Matlab)

В этом случае используются два подхода:

a)  логарифмическая амплитудно-фазовая частотная характеристика неизменяемой части апроксимируется кусочно-линейной зависимостью и аналитически определяются узловые частоты и передаточные функции корректирующего звена.

б)  задаются параметры корректирующего фильтра Т₁, Т₂, Т_к и подбираются необходимые значения для обеспечения требуемых запасов по амплитуде и по фазе.