Расчет и проектирование абсорбционной установки непрерывного действия для улавливания паров метанола из газовой смеси (воздушной) водой, страница 14

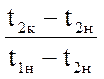P = ,                                                                (3.2.15)

P = 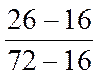= 0,179,

R = .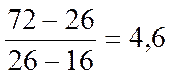

Подставив найденные значения Р и R, найдём коэффициенты η, δ по формулам (3.2.12), (3.2.13):

η = ,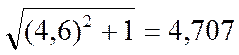

δ = .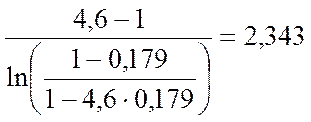

Тогда по формуле (3.2.11) определим поправку для среднелогарифмичекой разности температур:

ε_{Δ t} =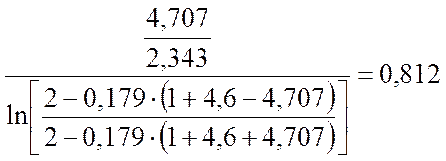

Т.о. среднелогарифмичекая разность температур с учётом поправки:

= 0,812 ∙ 20,715 = 16,883.

С учётом поправки ориентировочное значение площади поверхности теплообмена по формуле (3.2.10) составит 222,808 м² .

По таблице 2.3 /1/ выбираем  кожухотрубчатый шестиходовой холодильник со следующими характеристиками: диаметр кожуха D = 1200 мм, число труб n = 958, диаметр труб  d = 252 мм, длина труб L = 4 м, поверхность теплообмена F = 301 м².

Площадь сечения потока между перегородками (Таблица 2.3) /1/:

S_м = 0,165 м².

Проведем уточненный расчёт теплообменника.

1)  Межтрубное пространство.

 Критерий Рейнольдса для межтрубного пространства найдем по формуле:

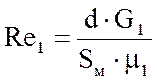,                                                      (3.2.16)

где Re₁ – критерий Рейнольдса для межтрубного пространства;

d – внешний диаметр труб теплообменника, м;

G₁ – массовый расход газовой смеси, кг/с;

S_м – площадь сечения потока между перегородками, м²;

μ₁ – динамический коэффициент вязкости газовой смеси при ее средней температуре 41,715 ⁰С, мПа∙с.

Массовый расход смеси газов равен:

,   (3.2.17)

где G₁ – массовый расход газовой смеси при ее средней температуре 41,715 ⁰C, кг/с;

V₁ – объемный расход газа, м³/с;

ρ₁ – плотность газовой смеси , кг/м³.

 Динамический коэффициен вязкости найдем по формуле:

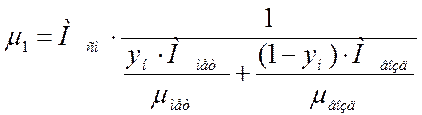, (3.2.18)

где μ₁– динамический коэффициент вязкости газовой смеси, Па∙с;

М_см – молекулярная масса газовой смеси, кг/кмоль;

y_н – начальная мольная доля метанола в воде, кмоль мет/кмоль см.;

М_мет – молекулярная масса метанола, кг/кмоль;

М_возд – молекулярная масса воздуха, кг/кмоль;

μ_мет, μ_возд – соответственно динамический коэффициент вязкости метанола и воздуха при средней температуре смеси, μ_мет = 1,055∙10^-5 Па∙c ,  μ_возд = 2,05∙10^-5 Па∙с /4/.

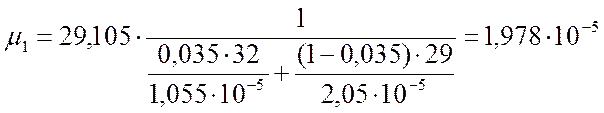
Поставим полученное значение в формулу (3.2.16):

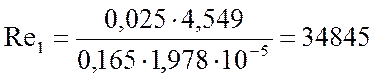
Коэффициент теплоотдачи для газовой смеси составит /4/:

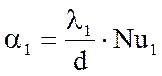, (3.2.19)

где α₁ – коэффициент теплоотдачи для газовой смеси, Вт/(м²∙К);

λ₁ – коэффициент теплопроводности газовой смеси при ее средней температуре 41,715 ⁰С, Вт/(м∙К);

d – внешний диаметр труб теплообменника, м;

Nu₁ – критерий Нуссельта для смеси газов.

Так как при теплообмене не происходит изменение агрегатного состояния и Re > 10⁴, то расчёт критерия Нуссельта произведем по фомуле /1/:

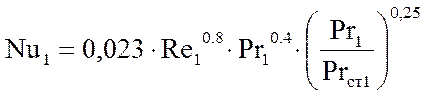, (3.2.20)

где Re₁ – критерий Рейнольдса для смеси газов;

Pr₁ – критерий Прандтля для газовой смеси;

Pr_ст1 – критерий Прандтля для стенки.

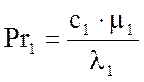,   (3.2.21)

где с₁ – теплоемкость газовой смеси;

μ₁ – динамический коэффициент вязкости газовой смеси при ее средней температуре 41,715 ⁰С, Па∙с;

λ₁ – коэффициент теплопроводности смеси при температуре 41,715 ⁰С, Вт/(м∙К).

Теплоемкость смеси была найдена выше.

Коэффициент теплопроводности смеси примем равным коэффициенту теплопроводности воздуха, так как физические свойства смеси близки к свойствам воздуха, тогда λ₁ = 0,0275 Вт/(м∙К) /5/.

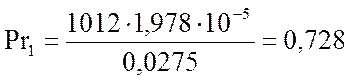
Выразим из формулы (3.2.20) значение критерия Нуссельта, поправкой 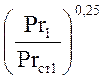можно пренебречь, т.к. для газов 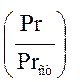= 1. Тогда критерий Нуссельта:

Определим коэффициент теплоотдачи к газовой смеси:

α₁ = 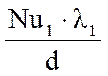,                      (3.2.22)               

где α₁ — коэффициент теплоотдачи к газовой смеси, Вт/(м²∙К).

α₁ =

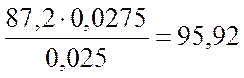
2)  Трубное пространство.

Критерий Рейнольдса для воды:

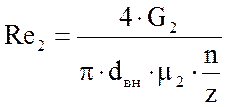 ,                                                                            (3.2.23)

где   Rе₂ – критерий Рейнольдса;

G₂ – массовый расход воды, кг/с;

d_вн – внутренний диаметр труб, м;

 μ₂ – динамический коэффициент вязкости воды при  t₂ =  21 ⁰С, мПа∙с;

z – число ходов теплообменника (z = 6);

n – общее число труб теплообменника (n = 958).

По Таблице XXXIX /4/ находим: μ ₂ = 0,980∙10^-3 мПа∙с.