Построение графика функции с применением сетки, обозначений по осям, заголовка, «легенды». Построение нейросети прямого распространения с одним скрытым слоем

                                                  Кафедра 106 МАИ

             Группа 01-314                                                  Студент:   Соколов В.М.

                                 Дополнительные главы информатики

                                         Лабораторная работа №4

                                                   Вариант №15

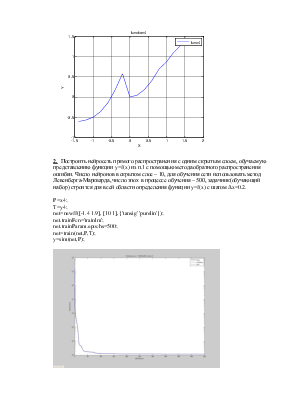
1.  Построить график функции при :

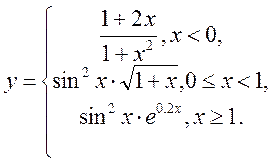
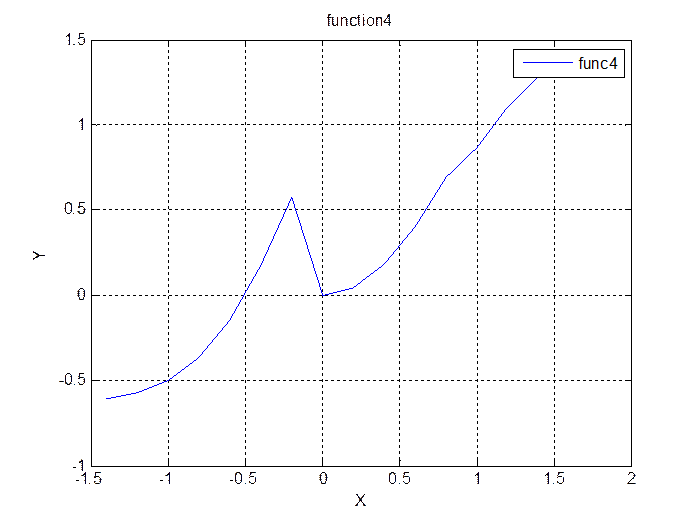
Должны присутствовать сетка, обозначения по осям, заголовок, «легенда».

 M-file

function y= func4(x);

if x<0

y=1+2*x/(1+x^2);

elseif x>=1

y=(sin(x)^2)*exp(0.2*x);

else

y=(sin(x)^2)*sqrt(1+x);

end

Функция

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end

plot(x4,y4)

grid on

xlabel('X');

ylabel('Y');

title('function4');

legend('func4');

print -dtiff fig4.tif

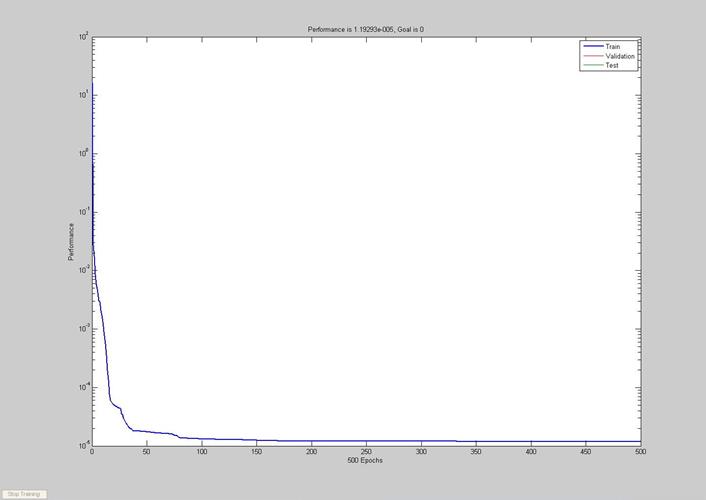
2.  Построить нейросеть прямого распространения с одним скрытым слоем, обучаемую представлению функции y=f(x) из п.1 с помощью метода обратного распространения ошибки. Число нейронов в скрытом слое – 10, для обучения сети использовать метод Левенберга-Маркварда, число эпох в процессе обучения – 500, задачник(обучающий набор) строится для всей области определения функции y=f(x) с шагом Δx=0.2.

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

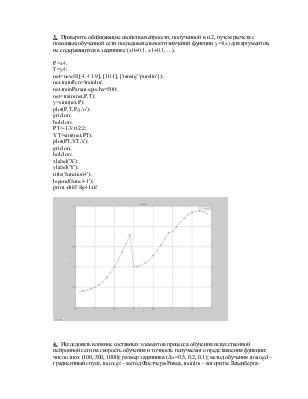
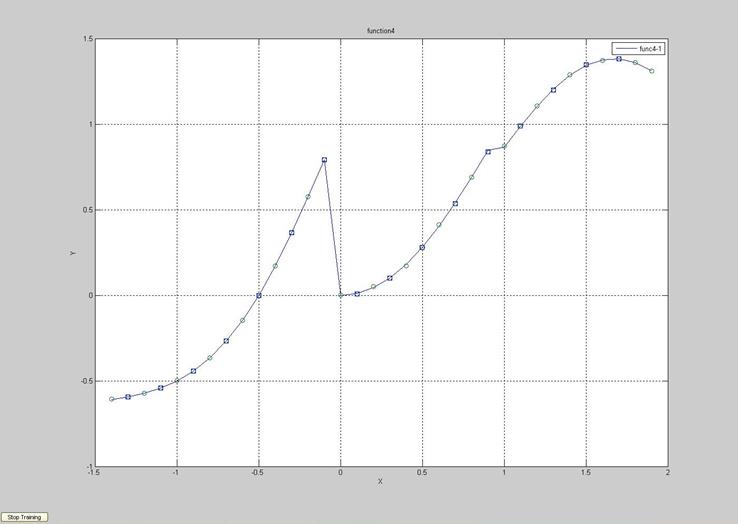
3.  Проверить обобщающие свойства нейросети, полученной в п.2, путем расчета с помощью обученной сети последовательности значений функции y=f(x) для аргументов, не содержащихся в задачнике (x0+0.1, x1+0.1, …).

 

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

PT=-1.3:0.2:2;

YT=sim(net,PT);

plot(PT,YT,'s');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-1');

print -dtiff fig41.tif

4.  Исследовать влияние составных элементов процесса обучения искусственной нейронной сети на скорость обучения и точность получаемого представления функции: число эпох (100, 500, 1000); размер задачника (Δx=0.5, 0.2, 0.1); метод обучения (traingd – градиентный спуск, traincgf – метод Флетчера-Ривса, trainlm – алгоритм Левенберга-Маркварда). Влияние числа эпох смотреть при Δx=0.2, алгоритм обучения trainlm; влияние размера задачника – для числа эпох 500, алгоритм обучения trainlm; влияние метода обучения – для числа эпох 500, при Δx=0.2.

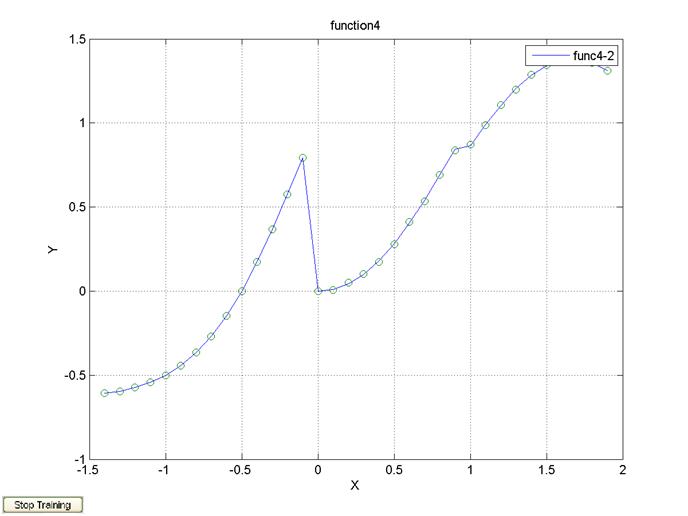
100 эпох, Δx=0.2, алгоритм обучения trainlm

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=100;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-2');

print -dtiff fig42.tif

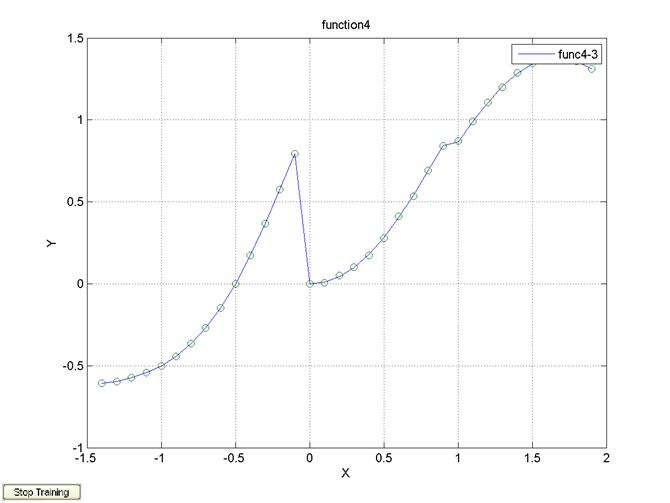
1000 эпох, Δx=0.2, алгоритм обучения trainlm

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=1000;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-3');

print -dtiff fig43.tif

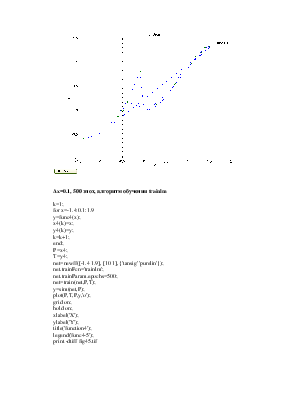
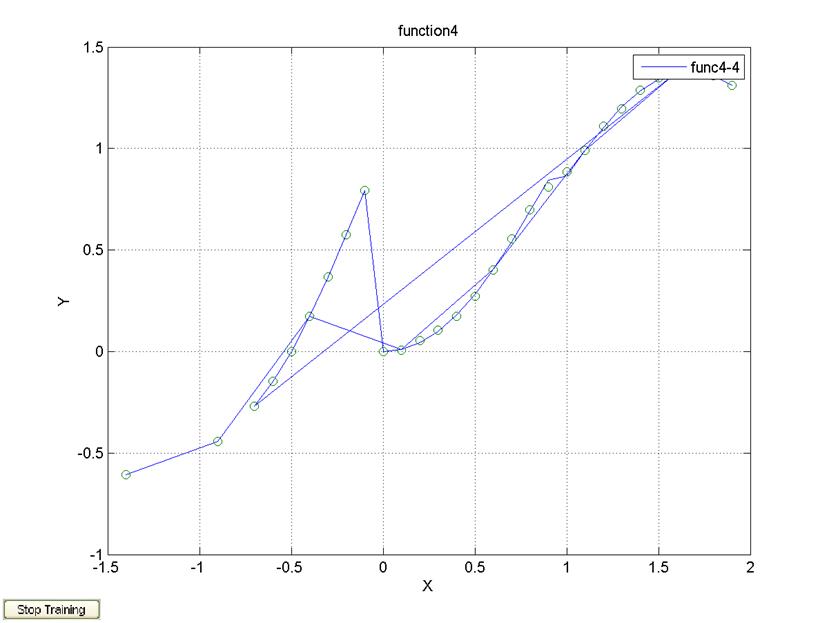
Δx=0.5, 500 эпох, алгоритм обучения trainlm

k=1;

for x=-1.4:0.5:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-4');

print -dtiff fig44.tif

Δx=0.1, 500 эпох, алгоритм обучения trainlm

k=1;

for x=-1.4:0.1:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');