Построение графика функции с применением сетки, обозначений по осям, заголовка, «легенды». Построение нейросети прямого распространения с одним скрытым слоем, страница 2

ylabel('Y');

title('function4');

legend('func4-5');

print -dtiff fig45.tif

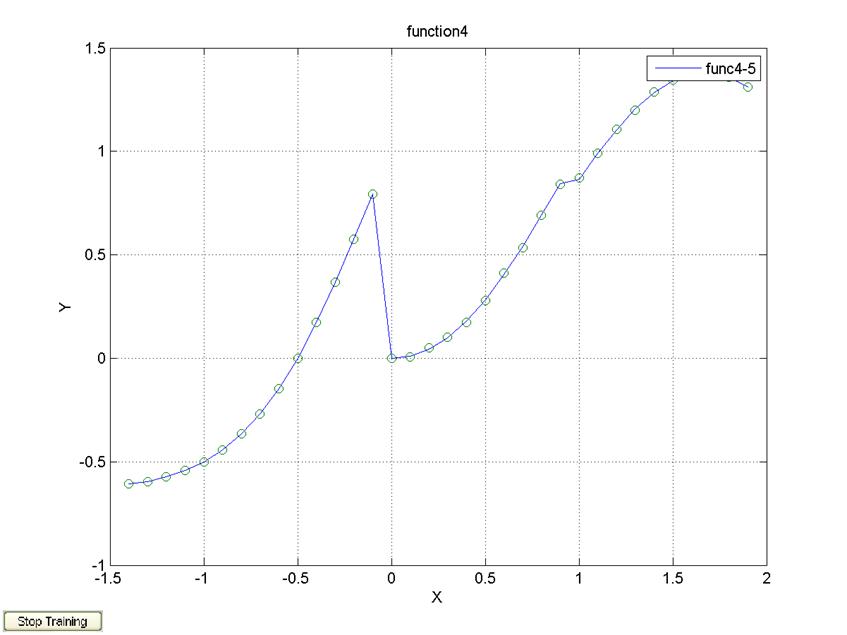
алгоритм обучения traingd, Δx=0.2, 500 эпох

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='traingd';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-6');

print -dtiff fig46.tif

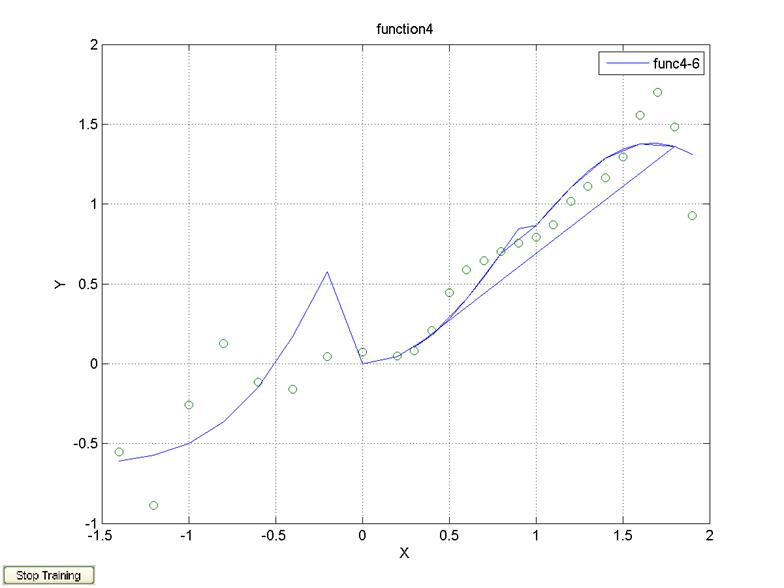
алгоритм обучения traincgf, Δx=0.2, 500 эпох

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'tansig' 'purelin'});

net.trainFcn='traincgf';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-7');

print -dtiff fig47.tif

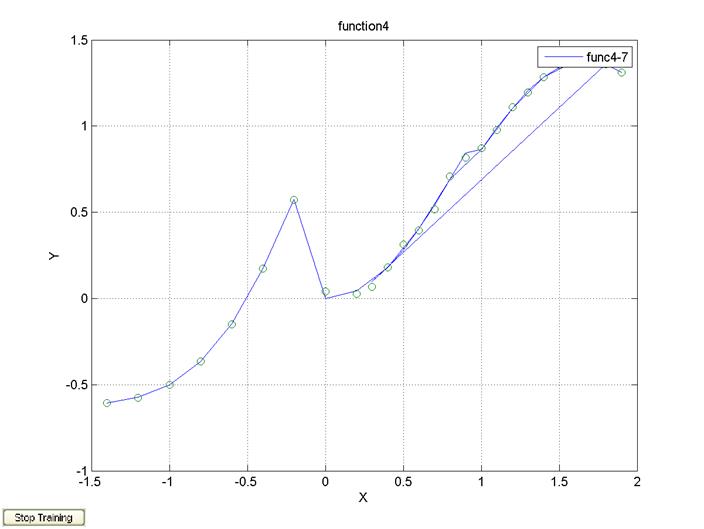
5.  Исследовать влияние архитектурной особенности нейросети на ее свойства: линейные и нелинейные активационные функции в нейронах скрытого слоя (число нейронов  - 10, число эпох – 500, Δx=0.2, алгоритм обучения trainlm); число нейронов в скрытом слое (1, 2, 5, 10, 20); число скрытых слоев (1,2). При анализе влияния числа скрытых слоев использовать сети с 10 нейронами в одном слое, а также с 5 нейронами в первом слое и 3 нейронами во втором для сети с двумя скрытыми слоями.

1 нейрон, 1 слой, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [1 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-8');

print -dtiff fig48.tif

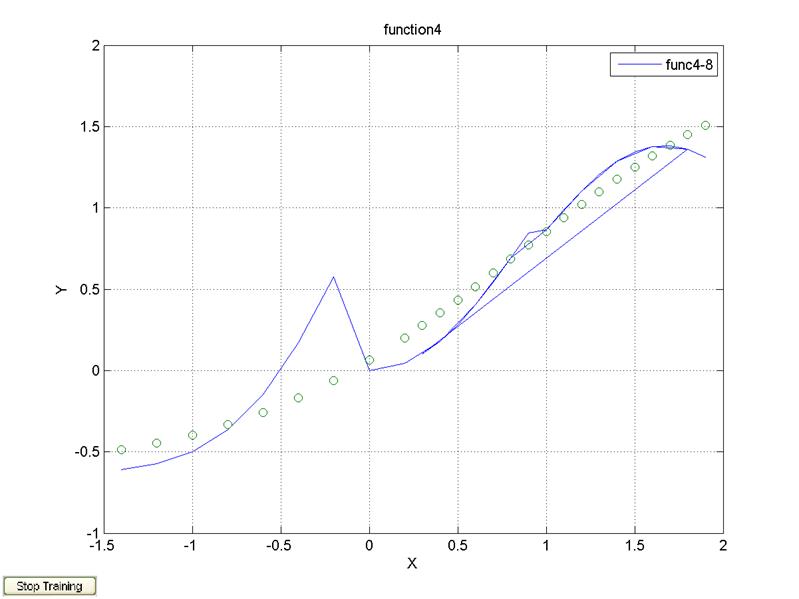
2 нейрона, 1 слой, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [2 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-9');

print -dtiff fig49.tif

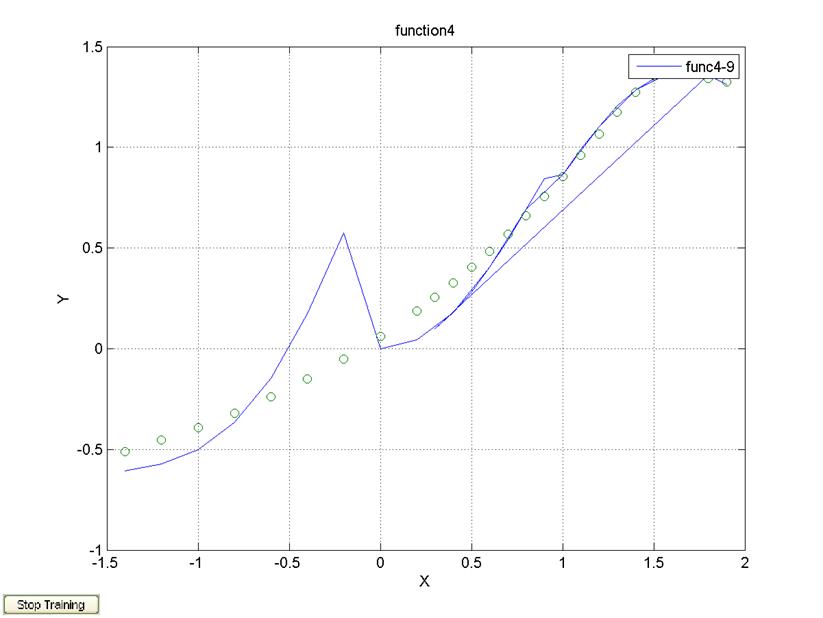
5 нейронов, 1 слой, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [5 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-10');

print -dtiff fig410.tif

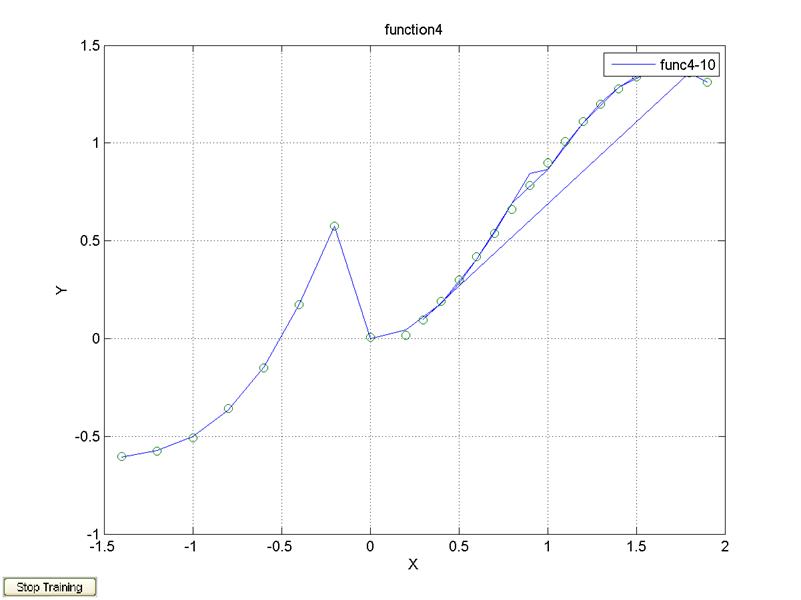
20 нейронов, 1 слой, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [20 1], {'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-11');

print -dtiff fig411.tif

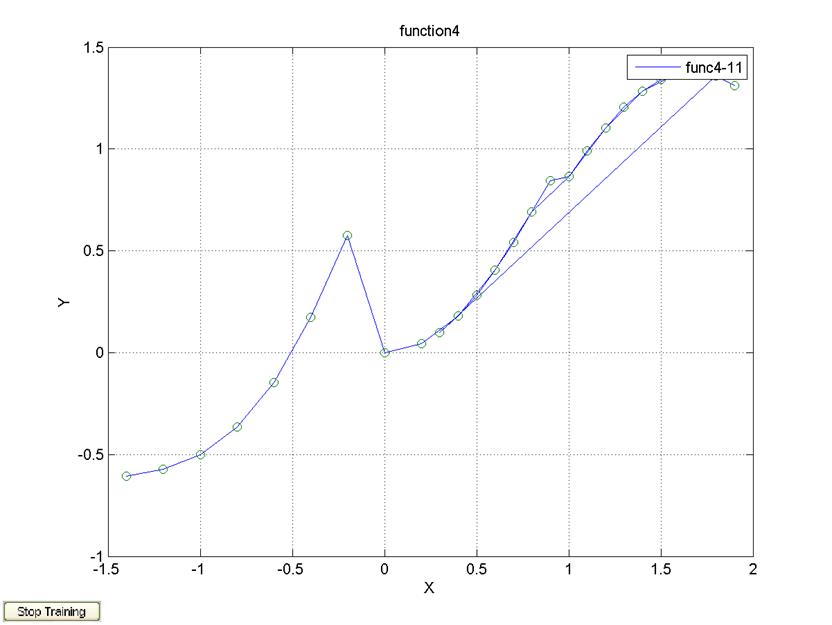
1 слой, 10 нейронов, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [10 1], {'purelin' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-12');

print -dtiff fig412.tif

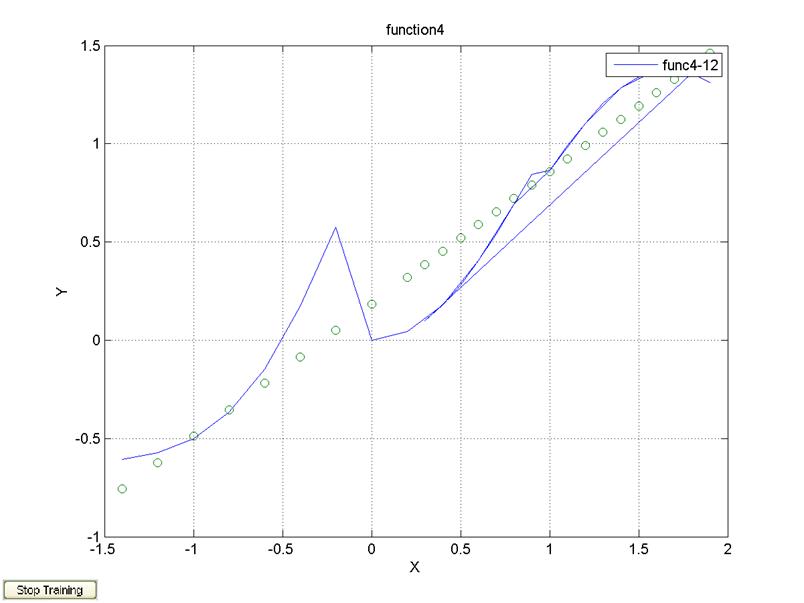
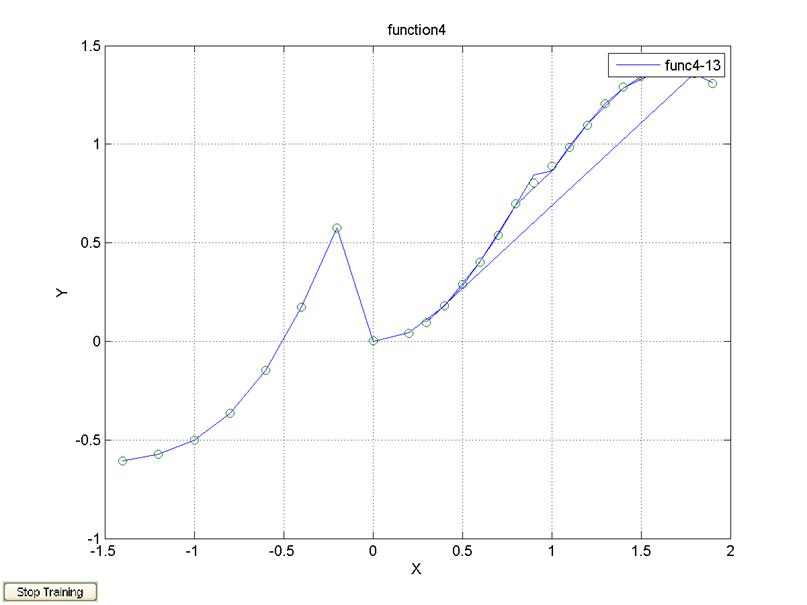
2 слоя,  5 нейронов,  3 нейрона, алгоритм обучения trainlm

k=1;

for x=-1.4:0.2:1.9

y=func4(x);

x4(k)=x;

y4(k)=y;

k=k+1;

end;

P=x4;

T=y4;

net=newff([-1.4 1.9], [5 3 1], {'tansig' 'tansig' 'purelin'});

net.trainFcn='trainlm';

net.trainParam.epochs=500;

net=train(net,P,T);

y=sim(net,P);

plot(P,T,P,y,'o');

grid on;

hold on;

xlabel('X');

ylabel('Y');

title('function4');

legend('func4-13');

print -dtiff fig413.tif