Анализ влияния атмосферной турбулентности на продольное движение самолета Боинг-747

                 Государственный    комитет    Российской   Федерации

по высшему образованию

 

Московский    Государственный   Авиационный  Институт

(технический   университет)

Кафедра 106

Динамики и управления летательных аппаратов.

Утверждено

руководитель

/ Чернышев А.В./

(подпись)

Защищено                                                                              

c оценкой

                 /                  /

    (дата)     (подпись)

Отчет

о курсовой работе по курсу

«Статистическая динамика»

____________

Тема: «Анализ влияния атмосферной турбулентности на продольное движение самолета Боинг-747».

Преподаватель:Чернышев А.В.

Выполнил студент группы 01-414

/ Доскалиев О.Г./

                                                                         (подпись)

                                                            Москва 2008 г.

Содержание.

1. Аннотация …………………………………………………………………………………..3
2. Вывод уравнений движения самолета……………………………………………………..4
3. Линеаризация математической модели……………………………………………………9
4. Вывод передаточных функций…………………………………………………………....11
5. Хар-ки турбулентной атмосферы. Описание метода вычисления дисперсии…...........14
6. Программная реализация………………………………………………………………….18
7. Результаты вычислений и выводы………………………………………………………..24
8. Список литературы………………………………………………………………………...27

Аннотация.

Цель курсовой работы – усвоить и углубить теоретические знания и приобрести практические навыки анализа функционирования динамических систем, подверженных воздействию случайных возмущений. В качестве динамической системы рассматривается продольное движение в турбулентной атмосфере.

Задание:

1. Разработать математическую модель полёта самолёта в турбулентной атмосфере.

·  Вывести линеаризованные уравнения продольного движения самолета при наличии  ветра.

·  Выбрать выходной параметр, закон регулирования системы улучшения устойчивости и управляемости.  

·  Из системы дифференциальных уравнений получить передаточную функцию, описывающую изменение высоты  в зависимости  от  скорости ветра.

2. Вычислить зависимости дисперсии высоты от режима полёта,

     параметров атмосферы и коэффициентов усиления системы управления.

3. Провести анализ полученных результатов.

Вывод уравнений движения самолета.

Уравнения движения самолета относительно инерциальной системы отсчета могут быть получены из основных теорем динамики твердого тела:

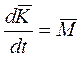
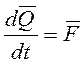
 и – главный вектор и главный момент относительно центра масс количества движения твердого тела (, );

 и   -  главный вектор и главный момент относительно центра масс внешних сил, действующих на твердое тело.

Если рассматривать самолет как твердое тело в произвольный момент времени, то к нему будут приложены:

внешние силы, действующие на систему, сила тяги двигателя  и внутренние кориолисовые силы инерции:

	(*)

 

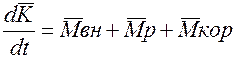
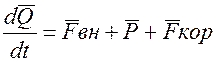
Исследовать движение самолета удобнее, пользуясь подвижными системами координат в начале с центром масс самолета. При проектировании производной по времени от какого-либо вектора  на оси любой подвижной системы координат Oxyz, вращающейся с угловой скоростью относительно выбранной системы отсчета (неподвижной), должны быть применены известные из векторного анализа формулы:

	(1)

 

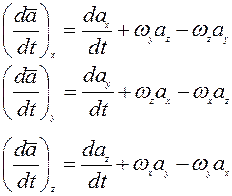
Пренебрегая скоростью и ускорением перемещения центра масс самолета относительно его корпуса, производная от количества движения по времени будет равна:

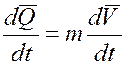
Учитываем правила векторного произведения  (1), разделяем полученные уравнения на проекции по осям XYZ, получим систему динамических уравнений движения в проекциях на оси системы координат, помещенных в центр масс самолета:

(2)

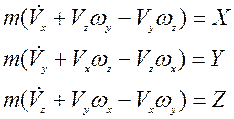
Векторное уравнение движения центра масс примет вид:

(3)

  

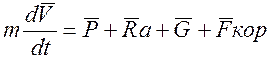
Наиболее простую и удобную форму система динамических уравнений движения центра масс самолета примет, если векторное уравнение спроектировать на оси траекторной системы координат ox_кy_кz_к.

Применяя формулу (2) для проектирования левой части уравнения (3) и учитывая, что , получим:

(4)

Где ,  - проекции на траекторные оси вектора угловой скорости  вращения траекторной системы координат относительно Земли.

- тяга двигателя, используя матрицу направляющих косинусов между осями связной и тракторной систем координат, проекции тяги двигателей оси траекторной системы получим в следующем виде:

;

;

,

- угол атаки,  - угол установки двигателя,  - угол скольжения, - скоростной угол крена.

Когда ветер отсутствует, траекторная система повернута относительно скоростной на угол - вокруг оси OX_a(X_k). С учетом этого проекции аэродинамической силы  на оси траекторной системы координат выражаются через проекции на скоростные оси:

Сила тяжести самолета приложены в его центре масс, направлена по местной вертикали вниз и расположена в плоскости ОХ_кУ_к траекторной системы координат, ее проекции на оси траекторной системы имеют вид: