








Завдання на 4 бали з дисципліни „Аналіз даних”
Завдання 1
Для даної вибірки обчислити за допомогою можливостей Excel
§ Середнє значення;
§ Виправлену дисперсію;
§ Виправлене середнє квадратичне відхилення.
Середнє значення;
СРЗНАЧ()
Виправлену дисперсію;
ДИСП()
Виправлене середнє квадратичне відхилення.
СТАНДОТКЛОН()
Завдання 2
Для даної вибірки обчислити за допомогою можливостей Excel
§ Моду;
§ Медіану;
§ Ассиметрію
§ Ексцесс
Моду;
МОДА()
Медіану;
МЕДИАНА()
Ассиметрію
СКОС()
Ексцесс
ЭКСЦЕСС()
Завдання 3
Для даної вибірки обчислити за допомогою можливостей Excel довірчий інтервал для математичного сподівання;

29,559
30,678
Завдання 4
Проведено 20 випробувань для визначення 5 параметрів регресійної моделі.
Відомо, що
SSзагльне =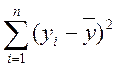 =
100 SSрегресійне =
=
100 SSрегресійне =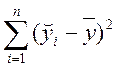 = 90
= 90
Визначити якість моделі та її адекватність з рівнем значущості 0,05.
У відповідь введіть:
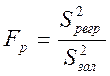 ; де
; де ![]() , k – кількість параметрів моделі.
Для парної лінійної регресії k=2, ( k-1)=1;
, k – кількість параметрів моделі.
Для парної лінійної регресії k=2, ( k-1)=1;
![]() , n –кількість
спостережень.
, n –кількість
спостережень.
Fкр=FРАСПОБР(α; k-1(5-1=4); n-k (20-5=15))
Якщо![]() , то модель адекватна
, то модель адекватна
0,90
+
3,375
3,06
+
Завдання 5
Для даної вибірки надані емпіричні та теоретичні частоти.
Перевірити за допомогою критерію Пірсона з рівнем значущості α=0,05, що вибірку можна описати за допомогою даного закону розподілу (обчислити за допомогою можливостей Excel )
У відповіді ввести:

Задовольняє
+ Так
Завдання 6
Два підприємства виготовляють пряжу : X – міцність на розрив (в кг/мм2) пряжі, виготовленої на підприємстві A, Y – міцність на розрив пряжі, виготовленої на підприємстві B. Із кожного підприємства була відібрана і перевірена пряжа із 10 котушок. Результати перевірки наведені в таблиці. Необхідно :
При рівні значимості ![]() використовуючи
F-критерій перевірити гіпотезу про рівність дисперсій.
використовуючи
F-критерій перевірити гіпотезу про рівність дисперсій.
|
X |
118,8 |
117,7 |
119,9 |
122,4 |
124,1 |
123,5 |
122,2 |
119,9 |
120,5 |
122,2 |
|
Y |
120,7 |
121,6 |
121,3 |
124,3 |
125,2 |
126,7 |
123,1 |
120,6 |
122,3 |
124,2 |
Перевіряємо гіпотези
H0: s2Х= s2У
Н1: s2Х ? s2У
У відповідь введіть:

Завдання 7
Два підприємства виготовляють пряжу : X – міцність на розрив (в кг/мм2) пряжі, виготовленої на підприємстві A, Y – міцність на розрив пряжі, виготовленої на підприємстві B. Із кожного підприємства була відібрана і перевірена пряжа із 10 котушок. Результати перевірки наведені в таблиці. Необхідно :
При рівні значимості ![]() використовуючи
t- критерій, при рівних дисперсіях перевірити: чи можна вважати
розходження між середніми X і Y значимими і обумовленими різними
технологічними процесами на підприємствах A і B;
використовуючи
t- критерій, при рівних дисперсіях перевірити: чи можна вважати
розходження між середніми X і Y значимими і обумовленими різними
технологічними процесами на підприємствах A і B;
|
118.8 |
117.7 |
119.9 |
122.4 |
124.1 |
123.5 |
122.2 |
119.9 |
120.5 |
122.2 |
|
120.7 |
121.6 |
124.3 |
124.3 |
125.2 |
126.7 |
123.1 |
122.6 |
122.3 |
124.2 |
Перевіряємо гіпотези
H0: Xср=Уср
Н1: Xср ? Уср
У відповіді введить:
1. знак відношення (<, >, =, < >);
2. значення t-статистики (з точністю до сотих);
3. t критичне двостороннє (з точністю до сотих);
4. “+”, якщо є розходження між середніми X і Y значимі і обумовленими різними технологічними процесами на підприємствах A і B, “-”, якщо немає;

Завдання 8
В таблиці наведена динаміка росту прибутку фірми за останні n років в процентах до базового року
|
Рік Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
|
Прибуток У |
118,3 |
132,6 |
149,4 |
170,2 |
190,5 |
221,4 |
248,3 |
275,0 |
300,0 |
|||
1. Розрахувати а0 и а1 для лінійної регресії y=a0+a1x використовуючи функцію ЛИНЕЙН. Записати отримане рівняння (ввести a0 и a1 з точністю до сотих).
2. Найти коефіцієнт детермінації (з точністю до тисячних).
3. Модель якісна чи ні?

Завдання 9
В таблиці наведена динаміка росту прибутку фірми за останні n років в процентах до базового року
|
Рік |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
|
Прибуток |
118,3 |
132,6 |
149,4 |
170,2 |
190,5 |
221,4 |
248,3 |
275,0 |
300,0 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.