В1={-9; 0; -75; 0; 0; 0; 5; 13,66; -12,5}Т, значок Т означает транспонирование.
 5.
предположим теперь, что в односторонней связи F
возникает реакция, а в связи Е она отсутствует. Составим уравнение равновесия
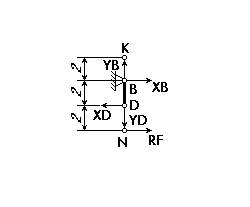
тел CD, NDBK и AFEC в этом случае. Силы, действующие на тела, показаны на рисунках
4, 5, 6.
При этом XC=X/C, YC=Y/C, XD=X/D, YD=Y/D, RF=R/F.
5.
предположим теперь, что в односторонней связи F
возникает реакция, а в связи Е она отсутствует. Составим уравнение равновесия
тел CD, NDBK и AFEC в этом случае. Силы, действующие на тела, показаны на рисунках
4, 5, 6.
При этом XC=X/C, YC=Y/C, XD=X/D, YD=Y/D, RF=R/F.
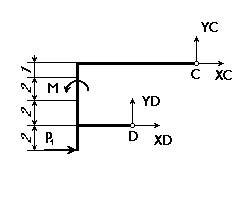
Рис.4 Рис.5
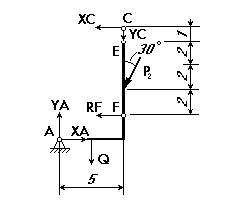
Рис.6
Так же, как и в случае возникновения реакции в односторонней связи Е, для каждого из рассматриваемых тел составим уравнения проекций и одно уравнение моментов. Тогда с учетом соотношений, для тела CD получаем:
ΣХК=0; ХC + ХD + P1=0,
ΣYК=0; YD + YC =0,
ΣМКC=0; 5XD – 5YD + 7 P1 + М =0.
Для тела NDBK:
ΣХК=0; XB – XD + RF=0,
ΣYК=0; YB - YD =0,
ΣМКK=0; 2XB- 4XD + 6RF =0.
Для тела AFEC:
ΣХК=0; XA - ХC - RF - P2∙sin300 =0,
ΣYК=0; YA – YC – Q – P2∙cos300 =0,
ΣМКC=0; 9XA - 5YA – 7RF + 2.5Q – 5P2∙sin300 =0.
 После вычислений получаем систему уравнений относительно неизвестных
XA, YA, XC,
YC, XD, YD,
XB, YB, RF:
После вычислений получаем систему уравнений относительно неизвестных
XA, YA, XC,
YC, XD, YD,
XB, YB, RF:
ХC + ХD = -9
YC + YD =0
5XD – 5YD = -75
XB – XD + RF=0
YB - YD =0,
2XB - 4XD + 6RF =0
ХA – XC - RF =5
YA – YC =13,66
9XA – 5YA - 7RF =12,5
Данная система уравнений в матричной форме имеет вид:
А2Х2=В2,

А2=
6. С помощью компьютерной программы С-9 определяем реакции внешних и внутренних связей. Результаты расчетов для случая возникновения реакции в односторонней связи Е представлены в таблице 1, а для случая возникновения реакции в связи F – в таблице 2.
|
XA |
YA |
XC |
YC |
XD |
YD |
XB |
YB |
RE |
|
2.97 |
2.14 |
-5.52 |
-11.52 |
-3.48 |
11.52 |
-6.97 |
11.52 |
3.48 |
Таблица 1.
|
XA |
YA |
XC |
YC |
XD |
YD |
XB |
YB |
RF |
|
2.97 |
12.59 |
4.93 |
-1.07 |
-13.93 |
1.07 |
-6.97 |
1.07 |
-6.97 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.