Определить реакции опор А и В, усилия во внутренних двусторонних связях С и D, и усилия в односторонних связях Е и F составной конструкции, изображённой на рисунке (размеры - в метрах).
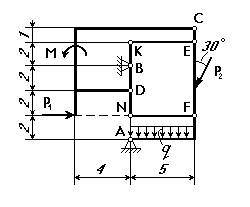
Дано:
Р1=9 кН,
Р2=10 кН,
М=12 кН∙м,
q=1 кН/м.
Решение:
1. По условию задачи при заданной схеме нагружения конструкции реакция возникает только в одной из односторонних связей Е или F. Предположим вначале, что в односторонней связи Е возникает реакция, а реакция связи F равна нулю.
Конструкция состоит из трех твёрдых тел CD, NDBK и AFEC, которые соединены между собой внутренними связями. Рассмотрим равновесие каждого из этих тел отдельно. Для каждого тела будем составлять два уравнения проекции и одно уравнение моментов.
2. Расчленим конструкцию. На рисунках 1, 2 и 3 показаны силы, действующие на тела CD, NDBK, AFEC соответственно. Внутренними связями являются связи С, D и Е . Реакции этих связей связаны соотношениями:XC=X/C, YC=Y/C, XD=X/D, YD=Y/D, RE=R/E.
Действие распределенных сил заменим действием сосредоточенной силы
Q=q∙5=1∙5=5 кН. Направление силы Q и точка её приложения показаны на рисунке 3.
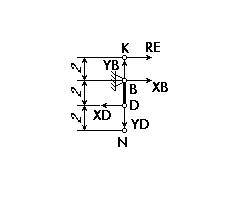
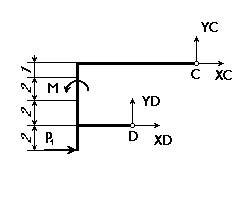
Рис.1 Рис. 2
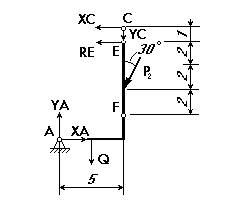
Рис.3
3. Составим уравнения равновесия тел CD, NDBK и AFEC. Предполагая, что ось Ох направлена горизонтально вправо, а ось Оу – вертикально вверх, запишем для каждого из указанных тел уравнения проекции на ось Ох, уравнения проекции на ось Оу и уравнения моментов относительно некоторой точки. Учитывая соотношения, для тела СD получаем:
ΣХК=0; ХC + ХD + P1=0,
ΣYК=0; YC + YD =0,
ΣМКC=0; 5XD – 5YD + 7 P1 + М =0.
Для тела NDBK:
ΣХК=0; XB – XD + RE=0,
ΣYК=0; YB - YD =0,
ΣМКK=0; 2XB- 4XD =0.
Для тела AFEC:
ΣХК=0; - ХC + XA - RE - P2∙sin300 =0,
ΣYК=0; YA – YC – Q – P2∙cos300 =0,
ΣМКC=0; 9XA - 5YA – RE + 2.5Q – 5P2∙sin300 =0.
 Перенося свободные члены полученных уравнений в правые части и
приводя необходимые вычисления, получаем систему девяти уравнений относительно
девяти неизвестных XA, YA, XC, YC, XD, YD, XB, YB, RE:
Перенося свободные члены полученных уравнений в правые части и
приводя необходимые вычисления, получаем систему девяти уравнений относительно
девяти неизвестных XA, YA, XC, YC, XD, YD, XB, YB, RE:
ХC + ХD = -9
YC + YD =0
5XD – 5YD = -75
XB – XD + RE=0
YB - YD =0,
2XB - 4XD =0
ХA – XC - RE =5
YA – YC =13,66
9XA – 5YA - RE =12,5
При составлении системы все вычисления производились с точностью до трех знаков после запятой.
4. Запишем в матричной форме систему уравнений равновесия для случая, когда возникает реакция в односторонней связи Е:
А1Х1=В1
XA YA XC YC XD YD XB YB RE
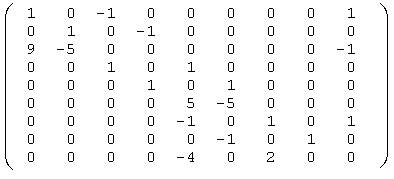
А1=
Х1={XA,YA,XC,YC,XD,YD,XB,YB,RE}Т
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.