






МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
Кафедра економіки та бізнес-адміністрування
Обов’язкове домашнє завдання
з дисципліни
«Методи ефективного управління економічними системами»
Виконав: студент IV курсу групи Едп-92
Татарченко А. С.
варіант № 10
Перевірила: Волк Ольга Миколаївна
Суми 2012
Дані дві функції: функція попиту за ціною q=23+19,4p та функція попиту за доходом q =-10,1-10,5I-9,3I2.Необхідно знайти еластичність попиту за ціною та доходом, при ціні 678 грн та доходу 6 тис. грнвідповідно.
Розв’язання:
1)Знайдемо еластичність попиту за ціною.
Для знаходження еластичності попиту за ціною скористаємося формулою:
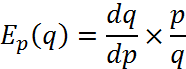
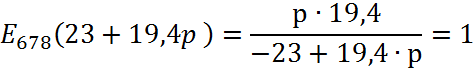
Висновок: Наш попит називають попит з одиничною еластичністю, тобто при зміні ціни на 1 % величина попиту буде 100 %.
2) Знайдемо еластичність попиту за доходом.
Для знаходження еластичності попиту за доходом скористаємося формулою:
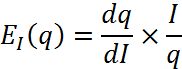
Де I – дохід,
![]() - функція попиту за доходом
- функція попиту за доходом
![]() - похідна від функції попиту по доходу
- похідна від функції попиту по доходу
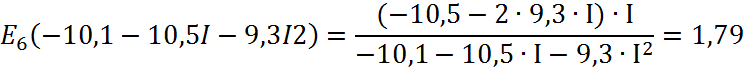
Висновок: Наша еластичність позитивна, а отже вона характеризує нормальні, якісні товари. При зміні доходу споживача на 1 % величина попиту зміниться на 179 %.
Задача 2
Споживач отримує дохід 7675, що витрачає на два види товарів. Ціни на товари дорівнюють 212 грн та 18 грн , мінімально необхідна кількість кожного виду товарів, що споживається в будь-якому випадку і не є предметом вибору дорівнює 1 од. та 4 од. відповідно. Відносна цінність товарів для споживача дорівнює 0,15 та 0,85. Визначте попит споживача, що буде максимізувати його корисність при заданому бюджетному обмеженні.
Розв’язання:
Для максимізації корисності попиту споживача будемо використовувати модель Р. Стоуна. Ця функція має вигляд:
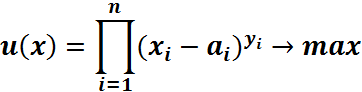
Де ![]() - невідома кількість i –го блага,
- невідома кількість i –го блага,
![]() - мінімальна необхідна кількість i –го блага,
- мінімальна необхідна кількість i –го блага,
![]() – характеризує відносну цінність благ для споживача.
– характеризує відносну цінність благ для споживача.
![]()
Щоб набір {![]() } міг бути повністю придбаний, необхідно, щоб дохід був більше
кількості коштів, необхідних для придбання цього набору:
} міг бути повністю придбаний, необхідно, щоб дохід був більше
кількості коштів, необхідних для придбання цього набору: ![]()
![]()
Використовуючи функцію попиту знайдемо невідому кількість товару за формулою:
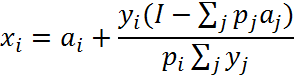
Де ![]() - мінімальна необхідна кількість i –го блага,
- мінімальна необхідна кількість i –го блага,
![]() – характеризує відносну цінність благ для споживача,
– характеризує відносну цінність благ для споживача,
![]() - дохід,
- дохід,
![]() – ціна.
– ціна.
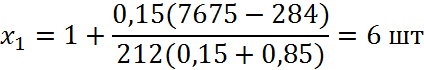
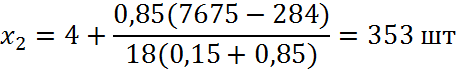
Тепер знаходимо максимальну корисність:
![]()
Висновок: Для того, щоб отримати максимальну корисність – 146, від попиту, споживачу необхідно придбати 6 одиниць першого товару і 353 одиниці другого товару.
Для заданої виробничої функції Y=f(x1;x2), де х1, х2 – витрати ресурсів, необхідно визначити максимальний випуск та витрати ресурсів, що забезпечують цей випуск.
|
10 |
Y = –6,9x12 + 25,1x1 + 2,2x1x2 + 13,1x2 – 2,1x22 |
Розв’язання:
Це задача на знаходження безумовного екстремуму. Знаходимо часткові похідні виробничої функції та прирівнюємо їх до нуля.
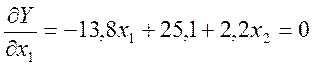 ;
;
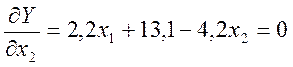 .
.
Розв’язуємо отриману систему двох рівнянь щодо двох змінних.
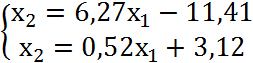
![]()
Одержуємо відповідь
х1 = 2,53; х2 = 4,44
.
Перевіримо, чи є знайдена екстремальна точка точкою максимуму, для цього повинні виконуватися умови:
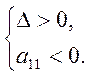
У даному випадку
 ,
,
тому умови виконані, отже, знайдена точка максимуму.
Знаходимо максимальний випуск:
![]() .
.
Висновок: При заданій виробничій функції максимальний випуск продукції буде складати 60,82 (одиниць вимірювання). Щоб досягти такого випуску необхідно затратити 2,53 (одиниць вимірювання) першого ресурсу та 4,44(одиниць вимірювання) другого ресурсу.
Задача 4
Економічна система складається із 4 підприємств, боргові відносини яких описані в матриці боргів. Необхідно визначити 1) сумарні боргові зобов’язання; 2) сальдо кожного підприємства; 3) сумарне сальдо; 4) вирішити задачу взаємозаліку боргів підприємств; 5) зробити перевірку.
|
10 |
|
Для початку побудуємо розгорнуту матрицю:
|
1 |
2 |
3 |
4 |
|
|
1 |
0 |
-300 |
70 |
50 |
|
2 |
300 |
0 |
130 |
340 |
|
3 |
-70 |
-130 |
0 |
-50 |
|
4 |
-50 |
-340 |
50 |
0 |
1) Визначимо сумарні боргові зобов’язання:
Сумарні боргові зобов’язання визначаються за формулою:
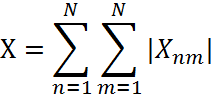
Де ![]() – борг n-го підприємства m-му:
– борг n-го підприємства m-му: ![]()
X – сума
всіх боргів
N – кількість підприємств
Якщо:
![]() < 0 – підприємство n-боржник
< 0 – підприємство n-боржник
![]() > 0 – підприємство n-кредитор
> 0 – підприємство n-кредитор
![]() = 0 – підприємство не має боргу
= 0 – підприємство не має боргу
Х=0+300+70+50+300+0+130+0+340+70+130+0+50+50+340+50+0=1880
2) Порахуємо сальдо кожного підприємства:
Сальдо підприємства рахується за формулою:
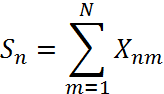
де
![]() - сальдо підприємства
- сальдо підприємства
![]() - борг n–го підприємства m–му
- борг n–го підприємства m–му
Якщо:
![]() < 0
- у підприємства більше боргів ,ніж кредитів
< 0
- у підприємства більше боргів ,ніж кредитів
![]() > 0
- підприємство кредитор
> 0
- підприємство кредитор
![]() = 0 - підприємство є нейтральним до боргів системи
= 0 - підприємство є нейтральним до боргів системи
![]() =0-300+70+50=-180- боржник
=0-300+70+50=-180- боржник
![]() =300+0+130+340=770- кредитор
=300+0+130+340=770- кредитор
![]() =-70-130+0-50=-250-боржник
=-70-130+0-50=-250-боржник
![]() =-50-340+50+0=-340-боржник
=-50-340+50+0=-340-боржник
3) Підрахуємо сумарне сальдо:
Абсолютне сальдо системи розраховується за формулою:
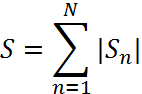
Де ![]() - сальдо підприємства.
- сальдо підприємства.
S=180+770+250+340=1540
4)Задача взаємозаліку боргів підприємства:
Нові борги підприємства розраховуються за формулою:
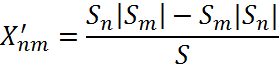
![]() - Сальдо підприємства
- Сальдо підприємства
S - сумарне сальдо
![]()
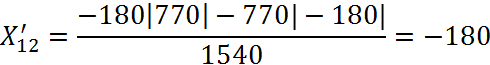
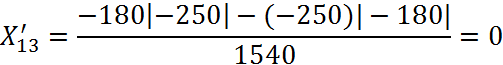
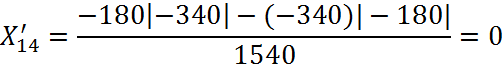
![]()
![]()
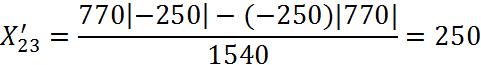
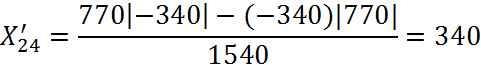
![]()
![]()
![]()
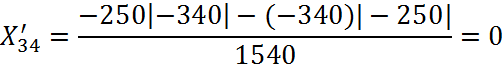
![]()
![]()
![]()
![]()
Будуємо матрицю взаємозаліку боргів:
|
1 |
2 |
3 |
4 |
|
|
1 |
0 |
-180 |
0 |
0 |
|
2 |
180 |
0 |
250 |
340 |
|
3 |
0 |
-250 |
0 |
0 |
|
4 |
0 |
-340 |
0 |
0 |
4) Робимо перевірку:
Для перевірки правильного перерозподілу боргів використовуємо умови взаємозаліку боргів:
1.
![]() відомі та визначаються підприємствами.
відомі та визначаються підприємствами.
2.
![]() не змінюється, тобто
не змінюється, тобто ![]() /
/
3.
Частина боргів ![]() списується, частина переадресовується, тобто у підприємства можуть
виникнути нові боржники і кредитори і зникнути старі.
списується, частина переадресовується, тобто у підприємства можуть
виникнути нові боржники і кредитори і зникнути старі.
Розрахуємо нові сальдо:
![]() =0-180+0+0=-180- боржник
=0-180+0+0=-180- боржник
![]() =180+0+250+340=770- кредитор
=180+0+250+340=770- кредитор
![]() =0-250+0+0=-250-боржник
=0-250+0+0=-250-боржник
![]() =0-340+0+0=-340-боржник
=0-340+0+0=-340-боржник
Підрахуємо сумарне сальдо:
S = 180+770+250+340=1540
Висновок: Як мибачимо сальдо кожного підприємства і сумарне сальдо залишилися без змін, перша та третя умова також виконуються, а отже взаємозалік боргів було проведено правильно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.