


Татарченко Аліна ІН‑91
Лабораторна робота №7
Варіант 10
1. Умова задачи.
Чисельно
розв’язати задачу Коші для диференціального
рівняння першого порядку з точністю ![]() =0,00001, використовуючи
метод Рунге- Кутта 4-го порядку.
=0,00001, використовуючи
метод Рунге- Кутта 4-го порядку.
![]()
2. Математичне обґрунтування алгоритму розв’язання задачи.
Якщо ![]() неперервна і обмежена разом зі своїми
четвертими похідними, то використовують метод четвертого порядку (метод
Рунге-Кутта). Він описується системою
таких п’яти співвідношень:
неперервна і обмежена разом зі своїми
четвертими похідними, то використовують метод четвертого порядку (метод
Рунге-Кутта). Він описується системою
таких п’яти співвідношень:
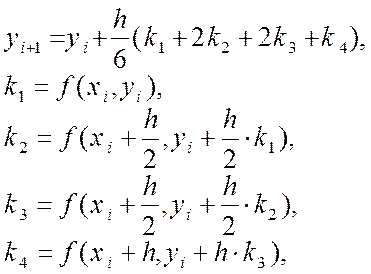 (
(![]() ).
).
Обчислювальна схема (алгоритм) методу Рунге-Кутта:
1
вибираємо початковий крок h на відрізку [a,b], задаємо точність ![]() ;
;
2
складаємо множину рівновіддалених точок (вузлів): ![]()
![]()
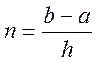 ;
;
3 визначаємо розв’язки yi+1 за формулами при кроці h і при кроці h/2, 0 ≤ i ≤ n-1;
4
перевіряємо нерівність ![]() ;
;
5
якщо ця нерівність виконується, то беремо ![]() і продовжуємо обчислення
і продовжуємо обчислення ![]() з тим самим кроком, якщо ні, то зменшуємо початковий крок h у два рази і переходимо до пункту 3.
з тим самим кроком, якщо ні, то зменшуємо початковий крок h у два рази і переходимо до пункту 3.
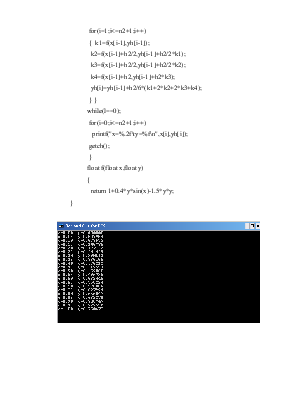
3. Програмна реалізація.
#include<stdio.h>
#include<conio.h>
#include<math.h>
#define m 200
float f(float x,float y);
void main()
{float yh[200],y[200],h=0.1,h2,a1=0,b1=1,a,c,y0=0,k1,k2,k3,k4,e,x[m];
int i,n,n2,l;
clrscr();
do{
l=1;
n=(b1-a1)/h;
for(i=0;i<=n+1;i++)
x[i]=a1+i*h;
y[0]=y0;
for(i=1;i<=n+1;i++)
{ k1=f(x[i-1],y[i-1]);
k2=f(x[i-1]+h/2,y[i-1]+h/2*k1);
k3=f(x[i-1]+h/2,y[i-1]+h/2*k2);
k4=f(x[i-1]+h,y[i-1]+h*k3);
y[i]=y[i-1]+h/6*(k1+2*k2+2*k3+k4);
}
h2=h/2;
n2=(b1-a1)/h2;
for(i=0;i<=n2+1;i++)
x[i]=a1+i*h2;
yh[0]=y0;
for(i=1;i<=n2+1;i++)
{ k1=f(x[i-1],yh[i-1]);
k2=f(x[i-1]+h2/2,yh[i-1]+h2/2*k1);
k3=f(x[i-1]+h2/2,yh[i-1]+h2/2*k2);
k4=f(x[i-1]+h2,yh[i-1]+h2*k3);
yh[i]=yh[i-1]+h2/6*(k1+2*k2+2*k3+k4);
} }
while(l==0);
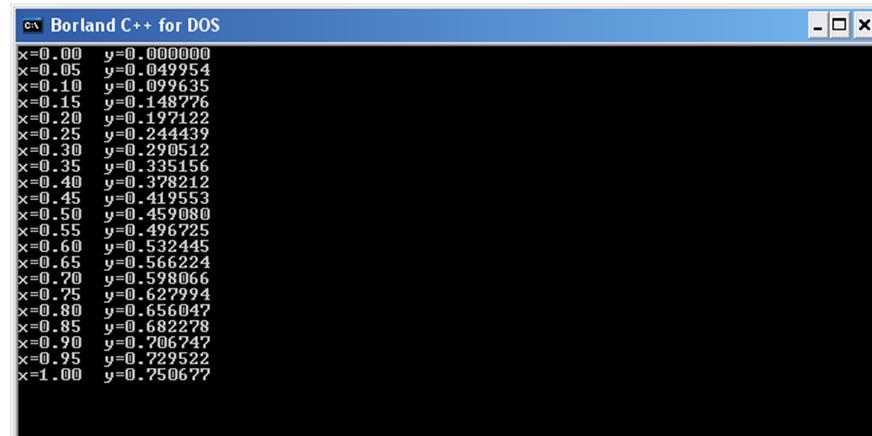
for(i=0;i<=n2+1;i++)
printf("x=%.2f\ty=%f\n",x[i],yh[i]);
getch();
}
float f(float x,float y)
{
return 1+0.4*y*sin(x)-1.5*y*y;
}
4. Пакетна реалізація.
Дану задачу можна вирішити за допомогою пакету Maple:
> eq:=diff(y(x),x)=1+0.4*y(x)*sin(x)-1.5*y(x)^2;
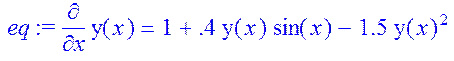
> cond:=y(0)=0;
![]()
> de:=dsolve({eq,cond},y(x),numeric);
![]()
> de(1);
![]()
5. Висновки.
Програмний і пакетний розв’язки системи збігаються, отже метод Рунге- Кутта 4-го порядку можна застосувати до даної задачі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.