Розв’язання системи нелінійних рівнянь з точністю 0,0001 методом градієнтного спуску (Лабораторна робота № 3)

Лабораторнаробота №3

З теми „Розв’язування систем лінійних алгебраїчних рівнянь”

Варіант №22

Студента групи Ін-52

Чайки Максима

1.  Умова задачі

Розв’язати  систему нелінійних рівнянь з точністю

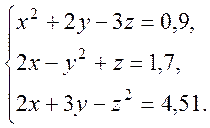
Для розв’язання системи рівнянь використовуємо метод градієнтного спуску.

Тоді:

 

                

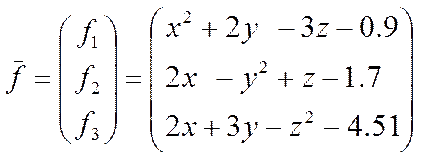
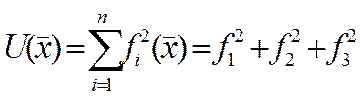
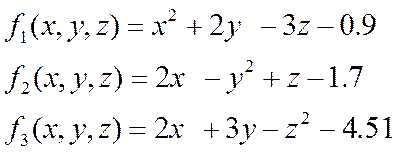
Функція  приймає нульове значення тільки тоді коли одночасно нулю дорівнюють функції . Тобто .

Розв’язок системи рівнянь буде точкою мінімуму функції   , так як в усіх інших точках  вона набуває додатних значень.

До цієї точки мінімуму будемо рухатися у напрямку протилежному до напрямку градієнта цієї функції.

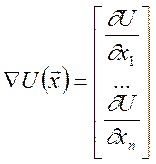- градієнт функції

> U:=(x^2+2*y-3*z-0.9)^2+(2*x-y^2+z-1.7)^2+(2*x+3*y-4.51)^2;

> Ux:=diff(U,x);

> Uy:=diff(U,y);

> Uz:=diff(U,z);

3. Текст програми

program gradient;

uses wincrt;

const

 eps=0.0001;

 lambda=-0.0001;

 n=3;

 type mas=array[1..n]of real;

    var x,y,z:real;

        Xp,nab,v:mas;

        i:integer;

function max(x:mas):real;

    var s:real;

       begin s:=abs(x[1]);

       for i:=2 to 4 do   if abs(x[i])>s then s:=abs(x[i]);

       max:=s;

    end;

Procedure add(var a,b:mas);

var

  i:integer;

 begin

  for i:=1 to n do

   begin

    a[i]:=a[i]+b[i];

   end;

 end;

   Procedure mult(a:mas;c:real;var v:mas );

var

  i:integer;

 begin

  for i:=1 to n do

   begin

    v[i]:=a[i]*c;

   end;

 end;

 procedure nabla(Xp:mas; var nab:mas);

   begin

nab[1]:=4*(Xp[1]*Xp[1]+2*Xp[2]-3*Xp[3]-0.9)*Xp[1]+16*Xp[1]-4*Xp[2]*Xp[2]+4*Xp[3]-24.84+12*Xp[2];

  nab[2]:=4*Xp[1]*Xp[1]+26*Xp[2]-12*Xp[3]-30.66-4*(2*Xp[1]-Xp[2]*Xp[2]+Xp[3]-1.7)*Xp[2]+12*Xp[1];

  nab[3]:=-6*Xp[1]*Xp[1]-12*Xp[2]+20*Xp[3]+2+4*Xp[1]-2*Xp[2]*Xp[2];

end;

begin

writeln('vvedite po4atkovi nabligennya');

write('x=');

readln(Xp[1]);

write('y=');

readln(Xp[2]);

write('z=');

readln(Xp[3]);

 repeat

   nabla(Xp,nab);

   mult(nab,lambda,v);

   add(Xp,v);

 until max(nab)<eps;

 writeln;

 writeln('vidpovidi:');

 writeln('x=',Xp[1]:1:4);

 writeln('y=',Xp[2]:1:4);

 writeln('z=',Xp[3]:1:4);

 end.

4.  Результати програми

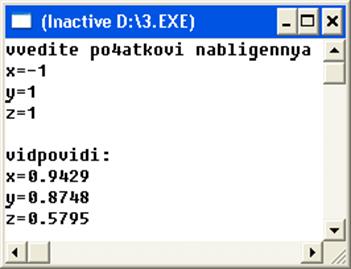
 Для заданої системи рівнянь ми отримали такі розв‘язки:

 Наприклад, при початковому наближенні х=-1  y=1 z=1, рухаючись у напрямі антиградієнта ми приходимо до кореня: