Розв’язання системи лінійних алгебраїчних рівнянь методом Зейделя (Лабораторна робота № 2)

Лабораторна робота №2

З теми „Розв’язування систем лінійних алгебраїчних рівнянь”

Варіант № 9

Студент групи ІН-61

Проскочило Владислав

1.  Умова задачі

Методом  Зейделя  розв’язати систему лінійних  алгебраїчних рівнянь  вигляду АХ=В із точністю до 0,0001.

	-0,81	-0,07	0,38	-0,21	0,81
9	-0,22	-0,92	0,11	0,33	0,64
	0,51	-0,07	-0,91	-0,11	-1,71
	0,33	-0,41	0,00	-1,00	1,21

2.  Математичний алгоритм

Спочатку для системи рівнянь перевіряємо умову збіжності послідовності ітераційної послідовності Х=φ(Х), де φ(Х)=СХ+D, Х- розв‘язок системи, С=[с_ij] - квадратна матриця порядку n:  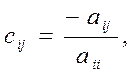   матриця D:      .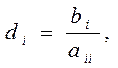

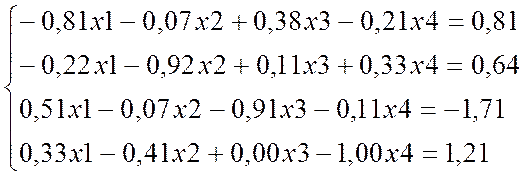     (1)

Для системи, записаної у вигляді (1), достатньою умовою збіжності є так зване діагональне переважання матриці А, тобто модулі діагональних коефіцієнтів для кожного рівняння системи не повинні бути менше, ніж сума модулів усіх інших коефіцієнтів при невідомих: .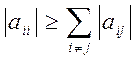

Для даної системи ця умова виконується.

Із кожного рівняння системи виражаємо діагональний елемент, таким чином ми приведемо систему до вигляду: Х=СХ+D.

Для системи, записаної у такому вигляді метод простих ітерацій збігається якщо для матриці С яка-небудь її норма менша 1.

 За методом Зейделя обчислення наступного наближення значення  x_i  використовуються обчислені раніше наближення невідомих x₁, x₂, …,   x_i-1 .

Ітераційний процес  методу Зейделя має вигляд:

                      

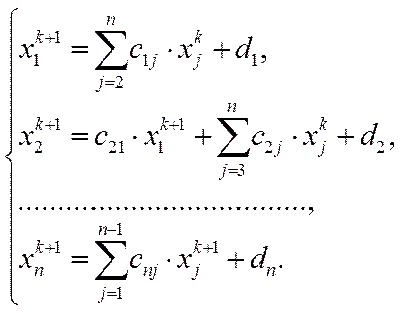
Ітераційний процес припиняють, якщо два послідовних наближення відрізняються менше від наперед заданого числа ∆ у змісті обраної норми:

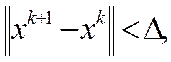
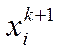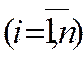тобто коли наближені розв’язки  і   стануть досить близькими і 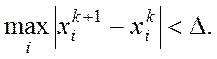 Величина ∆ пов'язана з точністю ε розв’язання системи співвідношенням 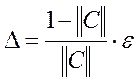, де - норма матриці з коефіцієнтів при невідомих у правих частинах рівнянь перетвореної системи: х=Сх+D.

3. Текст програми

program zendel;

uses wincrt;

const eps=0.0001;

          n=4;

type mas=array[1..4]of real;

var x,x1,b,d,summ:mas;

      i,j:integer;

      norm,M,s,Delta:real;

      A,C:array[1..n,1..n]of real;

function zeidel1(x:mas):real;

   begin

       zeidel1:=C[1,2]*x[2]+C[1,3]*x[3]+C[1,4]*x[4]+D[1]

   end;

function zeidel2(x:mas):real;

   begin

      zeidel2:=C[2,1]*x[1]+C[2,3]*x[3]+C[2,4]*x[4]+D[2]

   end;

function zeidel3(x:mas):real;

  begin

     zeidel3:=C[3,1]*x[1]+C[3,2]*x[2]+C[3,4]*x[4]+D[3]

   end;

function zeidel4(x:mas):real;

   begin

      zeidel4:=C[4,1]*x[1]+C[4,2]*x[2]+C[4,3]*x[3]+D[4]

  end;

function max(x,x1:mas):real;     {перевірка норми різниці наближень}

   var s:real;

   begin

       s:=abs(x[1]-x1[1]);

      for i:=2 to 4 do   if abs(x[i]-x1[i])>s then s:=abs(x[i]-x1[i]);

       max:=s;

   end;

begin

for i:=1 to n do     {введення коефіцієнтів }

     begin

       writeln ('koefizienty v ',i,' stroke matrizy A:');

       for j:=1 to n do

         readln (a[i,j]);

     end;

writeln;

writeln ('stolbez B:');

for i:=1 to n do

   readln (b[i]);

ClrScr;

for i:=1 to n do {перетворення матриць C i D}

     for j:=1 to n do

       begin

         if (i=j) then c[i,j]:=0

         else c[i,j]:=-a[i,j]/a[i,i];

       end;

  for i:=1 to n do

  d[i]:=b[i]/a[i,i];

   M:=0;  {обчислення норми матриці С}

  for i:=1 to 4 do

    begin

     if (abs(C[i,1])+abs(C[i,2])+abs(c[i,3])+abs(c[i,4]))>M

     then M:=abs(c[i,1])+abs(c[i,2])+abs(c[i,3])+abs(c[i,4]);

    end;

  norm:=M;

if abs(norm)<1 then    begin  {перевірка умови збіжності}

       Delta:=(1-norm)*eps/norm; {обчислення Дельта}

      for i:=1 to n do  {початкове наближення приймаємо за одиниці}

      x[i]:=1;

repeat    {ітераційна послідовність}

 for i:=1 to n do

  begin

      x1[i]:=x[i];

  end;

x[1]:=zeidel1(x);

x[2]:=zeidel2(x);

x[3]:=zeidel3(x);

x[4]:=zeidel4(x);

until max(x,x1)<delta;

clrscr;

writeln('otvet:');

for i:=1 to 4 do writeln('x',i,'=',x[i]:1:4);

end else writeln('ne shoditsya');

end.

4.  Результати програми

 Для заданої системи рівнянь ми отримали такі розв‘язки:

При розв‘язанні цієї системи рівнянь за допомогою Maple отримали такі результати:

> sys:={-0.81*x1-0.07*x2+0.38*x3-0.21*x4=0.81,-0.22*x1-0.92*x2+0.11*x3+0.33*x4=0.64,0.51*x1-0.07*x2-0.91*x3-0.11*x4=-1.71,0.33*x1-0.41*x2+0.00*x3-1.00*x4=1.21};

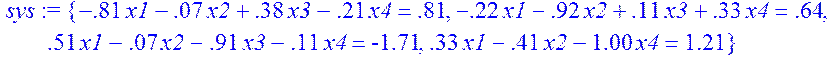
> X := solve( sys );

Для контрольного приклада для нашої програми можна обрати систему із наперед відомим розв‘язком, наприклад х1=х2=х3=х4=1 (початкове наближення обираємо х1=х2=х3=х4=0)

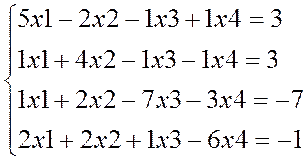
Відповідь: