Побудова моделей вхід-вихід і з простором станів за передатною функцією системи

Завдання

За передатною функцією системи

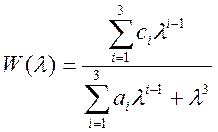
 побудувати:

1)  модель вхід-вихід;

2)  модель с простором станів;

3)  дослідити проблеми:

- керованості;

- спостережуваності;

- стійкості;

- асимптотичної стійкості.

      4) визначити потребу в декомпозиції системи.

Варіант
3	21,21	-1,32	0,63	4,27	-7,13	5,34

Розв’язок

1)  В загальному випадку модель вхід-вихід має вигляд:

  В нашому випадку модель вхід вихід має вигляд:

2)   Модель з простором станів має вигляд:

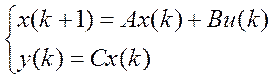                                                                 ( 1 )

В нашому випадку, , .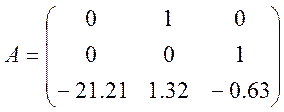

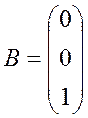3)  Дослідимо систему на керованість. Вона стаціонарна тому використаємо критерій Калмана, перевіримо умову rg(B, АВ,..., А^n-1B) = n, n=3. Використаємо пакет Maple:

> with(linalg):

> A:=matrix(3,3,[0,1,0,0,0,1,-21.21,     1.32,     -0.63]);

> B:=matrix(3,1,[0,0,1]);

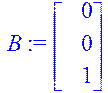
> AB:=evalm(A&*B);

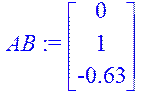
> A2B:=evalm(A&*A&*B);

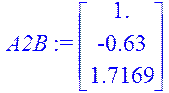
> K:=augment(B,AB,A2B);

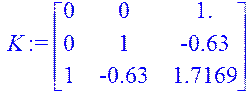
> rank(K);

Критерій Калмана виконується, тому система повністю керована.

Тепер дослідимо систему на спостережуваність.

Критерієм повної спостережуваності для стаціонарних систем має вигляд:

rg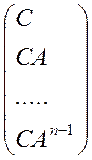= n

В нашому випадку необхідна умова має вигляд:

rg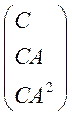= 3

Перевіримо цю умову за допомогою пакета Maple:

> C:=matrix(1,3,[4.27,    -7.13,    5.34]);

> CA:=evalm(C&*A);

> CA2:=evalm(C&*A&*A);

> GG:=stackmatrix(C,CA,CA2);

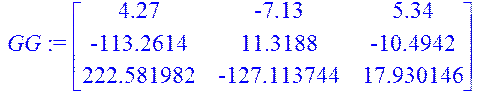
> rank(GG);

Необхідна умова виконується, тому система є повністю спостестережуваною.

Дослідимо систему на стійкість і асимптотичну стійкість.

Стійкість є внутрішньою властивістю лінійних систем, що не залежать від входу u(k), тому розглянемо математичну модель (1) при u(k) = 0 для всіх k, тобто

x(k + 1) = Ax(k).                                                                                     (2)

Існує Теорема. Для того щоб розв’язок системи (2) був стійким, необхідно і достатньо, щоб нульовий розв’язок системи рівнянь збурювань був стійким.

У термінах норми можна дати визначення стійкості за Ляпуновим. Виконаємо це стосовно системи (2). Нульовий розв’язок системи (2) називається стійким за Ляпуновим, якщо для будь-якого додатного  можна визначити таке , що з нерівності  при всіх k₁ > k₀ виконується нерівність 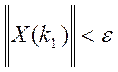 .   - відхилення початкових вхідних даних від нульових, .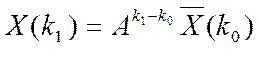

Перевіримо стійкість за допомогою Maple для k₁ = k₀+1 :

> X0:=matrix(3,1,[0.01,0.01,0.01]);

 X1:=evalm(A&*X0);norm(X0,2);norm(X1,2);

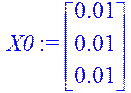
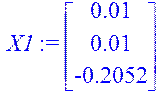
Мала зміна початкових даних викликала малу зміну результату, отже система є стійкою.

За теоремою Ляпунова: Для асимптотичної стійкості системи (2) необхідно і достатньо, щоб модулі всіх власних чисел матриці А були менше одиниці.

Перевіримо чи виконуються умови теореми. Характеристичний поліном нашої матриці А:

За допомогою Maple знайдемо  - власні значення :

 > charpoly(A,lambda);pp:=eigenvalues(A);

> evalc(abs(pp[1]));evalc(abs(pp[2]));evalc(abs(pp[3]));

Бачимо, що модулі всіх власних значень більші 1, тобто . Отже, наша система не є асимптотично стійкою.

4) Система повністю керована і повністю спостережувана, тому необхідності в декомпозиції не має.