Первісні корені та індекси. Загальні теореми, страница 4

c.  Нехай α=2. Тоді 2^α=4. Маємо φ(4)=2. Первісним коренем по модулю 2 буде, наприклад, 3≡-1(mod4). Числа 1⁰=(-1)⁰=1, (-1)¹=3(mod4) створюють зведену систему лишків по модулю 4.

d.  Нехай α≥3. Тоді 2^α≥8. Маємо φ(2^α)=2^α-1. Неважко помітити, що первісних коренів в цьому випадку немає; більш точно: показник, якому належить по модулю 2^α непарне число x, не більше 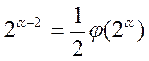. Дійсно, маємо

x²=1+8t₁

x⁴=1+16t₂

…

.

При цьому числа, що належать показнику 2^α-2, існують. Таким числом, наприклад, буде 5. Дійсно,

5=1+4

5²=1+8+16

5⁴=1+16+32u₂

…

звідки бачимо, що ні один з степенів 5¹, 5², 5⁴, …, не порівнянна з 1 по модулю 2^α.

Не важко помітити, що числа двох наступних рядків:

5⁰, 5¹, …,

-5⁰, -5¹, …,

утворюють зведену систему лишків по модулю 2^α. Дійсно, число цих чисел буде 2∙2^α-2=φ(2^α); Числа кожного взятого рядка між собою по модулю 2^α непорівнянні (1,b); нарешті, числа верхнього рядка непорівнянні з числами нижнього, так як перші по модулю 4 порівняні з 1, а другі з -1.

e.  Для зручності подальших досліджень ми виразимо результати b, c, d в більш одноманітній формі, яка буде придатна і в випадку α=0.

Нехай

c=1; c₀=1; якщо α=0 або α=1;

c=2; c₀=2^α-2; якщо α≥2.

(таким чином завжди cc₀=φ(2^α)) і нехай γ та γ₀ не залежать одне від одного пробігають найменші невід'ємні лишки

γ=0, …, c-1; γ₀=0, …, c₀-1

по модулям с та c₀. Тоді  перебігає зведену систему лишків по модулю 2^α.

f.  Порівняння

       (1)

має місце тоді і тільки тоді, коли

.

Дійсно, при α=0 теорема очевидна. Тому допустимо, що α>0. Нехай найменші невід’ємні лишки по модулям cта c₀ для чисел γта γ₀ будуть rта r₀, а для чисел γ’ та γ’₀ будуть r’ та r’₀. Беручи до уваги (c, 1) (-1 належить показнику c, а 5 належить показнику c₀), порівняння (1) має місце тоді і тільки тоді, коли , тобто (беручи до уваги пункт e) коли r=r’, r’=r’₀.

g.  Якщо

то система γ, γ₀ називається системою індексів числа a по модулю 2^α.

Беручи до уваги пункт e, будь-яке a, взаємно просте з 2^α (тобто непарне), має єдину систему індексів γ’, γ’₀ серед cc₀= φ(2^α)пар значень γ, γ₀ вказаних в e.

Знаючи систему γ’γ’₀, ми можемо вказати і всі системи індексів числа a; відповідно до f це будуть всі пари γ’γ’₀, складені з невід'ємних чисел класів

.

Безпосередньо з даного визначення системи індексів випливає, що числа з даною системою індексів γ, γ₀ утворюють клас чисел по модулю 2^α.

h.  Індекси добутку порівнянні по модулям c та c₀ з сумами індексів співмножників.

Дійсно, нехай γ(a), γ₀(a), …, γ(l), γ₀(l) – системи індексів чисел a, …, l. Маємо

.

З цього слідує, γ(a)+…+γ(l), γ₀(a)+…+γ₀(l) –індекси добутку a…l.

7.  Індекси по будь-якому зіставленому модулю

a.  Нехай  - канонічний розклад числа m. Нехай далі c та c₀ мають значення, вказані в (6,e); ; g_s– найменший первісний корінь по модулю .

b.  Якщо

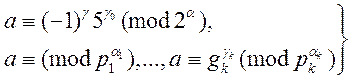       (1)

то система γ, γ₀, γ₁, …, γ_k називається системою індексів числа a по модулю m.

З такого визначення слідує, що γ, γ₀ - система індексів числа a по модулю 2^α, а γ₁, …, γ_k, - індекси числа a по модулям . Тому (6,g; 4,c) будь-яке a взаємно просте з m (тим самим воно взаємно просте і з усіма ), має єдину систему індексів γ’, γ’₀, γ’₁, …, γ’_k серед cc₀c₁…c_k=φ(m) систем γ, γ₀, γ₁, …, γ_k незалежно одне від одного перебігати найменші невід’ємні лишки по модулям c, c₀, c₁,…, c_k, а всі системи індексів числа a є всі системи γ, γ₀, γ₁, …, γ_k складені з невід'ємних чисел класів

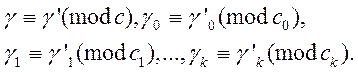
Числа a з даної системи індексів γ, γ₀, γ₁, …, γ_k можуть бути знайдені шляхом розв’язання системи (1), а значить, утворюють клас чисел по модулю m.

c.  Так як індекси γ, γ₀, γ₁, …, γ_k числа a по модулю m є індексами його відповідно по модулям , то вірна теорема

Індекси добутку порівнянні по модулям c, c₀, c₁,…, c_k з сумами індексів співмножників.

d.  Нехай τ=φ(2^α) при α≤2 та 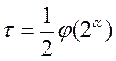 при α>2 і нехай h – найменше спільне кратне чисел τ, c₁, …,c_k. При будь-якому a, взаємно простому з m, порівняння a^h≡1 вірно по всім модулям , значить це порівняння вірно і по модулю m. Тому a не може бути первісним коренем по модулю m в тих випадках, коли h<φ(m). Але останнє має місце при α>2, при k>1, а також при α=2, k=1. Тому для m>1 первісні корені можуть існувати лише в випадках . Але якраз для цих випадків існування первісних коренів було доведено вище. Тому

Всі випадки, коли існують первісні корені по модулю m, які більше за 1, є

.

Запитання для самоперевірки

1.  Що таке первісний корінь?

2.  Поняття «індексу».

3.  Що представляють собою таблиці індексів?

4.  Число чисел та число первісних коренів, які належать показнику δ  в зведеній системі лишків по модулю m.

5.  Система індексів числа a по модулю m.