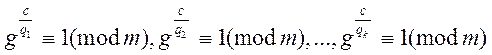Первісні корені та індекси. Загальні теореми, страница 2

        (1)

Дійсно, якщо g- первісний корінь, то тим самим він не може задовольняти ні одну з конгруенцій (1).

не задовольняло ні одну з конгруенцій.

, ми мали б 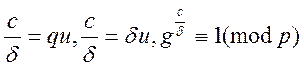, що протирічить нашому припущенню. Значить, δ=c та g- первісний корінь.

Приклад 1.

Нехай m=41. Маємо φ(41)=40=2³∙5 ,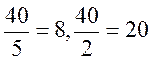. Отже, для того, щоб число gкотре не ділиться на 41, було первісним коренем по модулю 41, необхідно і достатньо, щоб це g не задовольняло ні одну з конгруенцій.

g⁸≡1(mod41), g²⁰≡1(mod41)            (2)

Але підставляючи числа 2,3,4,…, знаходимо (по модулю 41)

2⁸≡10, 3⁸≡1, 4⁸≡18, 5⁸≡18, 6⁸≡10

2²⁰≡1, 4²⁰≡1, 5²⁰≡1, 6²⁰≡40

Звідси бачимо, що числа 2, 3, 4, 5 не первісні корені, так як кожне з них не задовольняє, хоча б, одній з конгруенцій (2).

Приклад 2

Нехай m=1681=41².Первісний корінь і тут можна було б знайти, користуючись загальною теоремою. Але ми можемо знайти його легше, використовуючи теорему (2,e). Знаючи вже (приклад 1), що первісний корінь по модулю 41 рівний 6, знаходимо

6⁴⁰=1=41(3+41l)

(6+41t)⁴⁰=1+41(3+41l-6³⁹t+41T)=1+41u

Для того, щоб uне ділилось на 41 достатнь взяти t=0. Тому в якості первісного кореня по модулю 1681 можно взяти число 6+41∙0=6

Приклад 3

Нехай m=3362=2∙1681. Первісний корінь і тут можно було б знайти використовуючи загальну теорему, але ми знайдемо його простіше, використовуючи (2,f). Знаючи вже (приклад 2), що первісний корінь по модулю 1681 це 6, в якості первісного кореня по модулю 3362 можно взяти непарне з чисел 6,6+1681, тобто число 1687.

4.  Індекси по модулям p^αта p^2α

a.  Нехай p – просте непарне, α≥1; m – одне з чисел p^αта p^2α; c= φ(m), g – первісний корінь по модулю m.

b.  Якщо γ пробігає найменші додатні лишки  γ = 0, 1, … , c-1 по модулю c, то g^γ пробігає дану систему лишків по модулю m.

Дійсно, g^γ пробігає c чисел, взаємно простих з m, та маючи на увазі (b, 1), непорівнянних по модулю m.

c.  Для чисел a, взаємно простих з m, введемо поняття про індекс, яке представляє собою аналогію логарифму; при цьому первісний корінь грає роль, аналогічну ролі основи логарифмів.

Якщо

a≡g^γ(mod m)

(вважаємо, що γ≥0), то γ зветься індексом числа a по модулю m з основою g та позначається символом γ=ind_ga.

Враховуючи(4,b) всяке a, взаємно просте з m, має певний єдиний індекс γ' серед чисел ряду

γ = 0, 1, … , c-1

Знаючи γ', ми можемо вказати і всі індекси числа a; згідно з (1,c) це будуть всі невід`ємні числа класу

γ≡γ'(modc)

Безпосередньо з даного визначення індексу слідує, що числа з даним індексом γ утворюють клас чисел по модулю m.

d.  Маємо

Ind ab…l ≡ ind a + ind b + … +ind l(mod c)

також

ind aⁿ ≡ n ind a(mod c)

Дійсно,

a ≡ g^{ind a}(mod m), b ≡ g^{ind b}(mod m), … ,l ≡ g^{ind l}(mod m)

звідки, перемножуючи, знаходимо

ab…l≡ g^{inda + indb + … + ind l}(mod m)

Отже, ind a + ind b + … + ind l – один з індексів добутку ab…l.

e.  Для кожного модуля p складені так звані таблиці індексів. Це дві таблиці; перша – для знаходження індексу по числу, друга – для знаходження числа по індексу. Таблиці містять найменші додатні лишки чисел (зведена система) та їх найменших індексів (повна система) по модулям p та c = φ(p) = p-1.

Приклад. Побудуємо вказані таблиці, для модуля p=41.У попередніх прикладах було показано, що первісним коренем по модулю 41 буде g=6; його ми візьмемо  за основу індексів. Знаходимо (беруться конгруенції по модулю 41):

6⁰ ≡  1   6⁸ ≡ 10    6¹⁶ ≡ 18  6²⁴ ≡ 16   6³² ≡ 37

6¹ ≡  6   6⁹ ≡ 19    6¹⁷ ≡ 26  6²⁵ ≡ 14   6³³ ≡ 17

6² ≡ 36  6¹⁰ ≡ 32   6¹⁸ ≡ 33  6²⁶ ≡  2    6³⁴ ≡ 20

6³ ≡ 11  6¹¹ ≡ 28   6¹⁹ ≡ 34  6²⁷ ≡ 12   6³⁵ ≡ 38

6⁴ ≡ 25  6¹² ≡  4    6²⁰ ≡ 40  6²⁸ ≡ 31   6³⁶ ≡ 23

6⁵ ≡ 27  6¹³ ≡ 24   6²¹ ≡ 35  6²⁹ ≡ 22   6³⁷ ≡ 15

6⁶ ≡ 39  6¹⁴ ≡ 21   6²² ≡  5   6³⁰ ≡  9    6³⁸ ≡ 8

6⁷ ≡ 29  6¹⁵ ≡  3    6²³ ≡ 30  6³¹ ≡ 13   6³⁹ ≡ 7

Отже вказані таблиці будуть

P=41, p-1=2³·5, g=6

N	0		1	2	3	4			5	6	7	8	9
0 1 2 3 4		8 34 23 20	0 3 14 28	26 27 19 10	15 31 36 18		12 25 13 19	22 37 4 21		1 24 17 2	39 33 5 32	38 16 11 35	30 9 7 6