Операція. Математична модель операції. Методи оптимізації. Дифференцируемые выпуклые функции, страница 3

Т Пусть скалярная функция  дифференцируема на выпуклом множестве . Тогда для выпуклости функции  на  необходимо и достаточно, чтобы для любых двух точек  выполнялось неравенство

, де ,  – градиент функции ,  – скалярное произведение векторов.

Для строгой выпуклости функции  данное неравенство приобретает вид строгого неравенства.

Т Для того, чтобы дважды дифференцируемая на открытом выпуклом множестве  функция была выпуклой, необходимо и достаточно, чтобы ее матрица Гессе  была неотрицательно определённой в любой точке .

Т Необходимым и достаточным условием неотрицательной определенности симметрической матрицы является неотрицательность ее диагональных миноров.

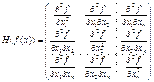
16.Функция  называется унимодальной на отрезке , если она непрерывна на  и существуют числа  и , , такие, что:

1) если , то  монотонно убывает при ;

2) если , то ;

3) если  то  монотонно возрастает при .

 Метод перебора

Разобьем отрезок  на  равных частей точками деления , . Вычислив значения  в точках , путем сравнения найдем точку , для которой .                                                                                             Далее, положим .

число отрезков разбиения  необходимо выбрать из условия , т.е. .

точность решения ,которую обеспечивает метод перебора в результате  вычислений  будет

Методы исключения отрезков

Первый метод деления отрезка пополам (дихотомии).

                                    , где  – малое число.

Шаг 1. Определить  и  по формулам (3.4). Вычислить и .

Шаг 2. Сравнить  и . Если ,то перейти к отрезку , положив , иначе – к отрезку , положив .

Шаг 3. Найти достигнутую точность . Если , то перейти к следующей итерации, вернувшись к шагу 1. Если , то завершить поиск , перейдя к шагу 4.

Шаг 4. Положить

Метод золотого сечения.

; .                              Шаг 1. Найти  и  по формулам (3.7). Вычислить  и . Положить , .

Шаг 2. Проверка на окончание поиска: если , то перейти к шагу 3, иначе – к шагу 4.

Шаг 3. Переход к новому отрезку и новым пробным точкам. Если , то положить , , ,  и вычислить , иначе – положить , , ,  и вычислить .

Положить  и перейти к шагу 2.

Шаг 4. Окончание поиска: положить , .

Сравнение методов исключения отрезков и перебора. При срав­нении прямых методов минимизации обычно учитывают количество  значений , гарантирующее заданную точность определения точки  тем или иным методом. Чем меньше , тем эффективнее считается метод. наиболее эффектив­ным из сравниваемых методов является метод золотого сечения, за ним идут методы деления отрезка пополам и наименее эффе метод перебора.

Багатокритеріальна задача в.о. увазі, що для отримання рішення задачі в.о. потрібно врахувати багато критеріїв, і відповідно врахувати їх у моделі, а значить і у функції мети. В такому випадку функція мети є багатокритеріальної і сепарабельному.

Строго выпуклое множество – это выпуклое множество, у которого вершины отсутствуют.

Линейная комбинация строго выпуклая, если все .

Выпуклый многогранник – выпуклое множество, ограниченное совокупностью гиперплоскостей.

Точка Х называется вершиной выпуклого многогранника, если она не представима строго выпуклой комбинацией других точек многогранника.

Теорема 1Выпуклая оболочка множества Е совпадает с множеством всех выпуклых комбинаций элементов множества Е.

Теорема Каратеодори.

Любую точку Х выпуклой оболочки произвольного множества  можно представить как линейную комбинацию элементов множества Е, количество слагаемых которой

Свойства выпуклых функций.

Теорема 1

Линейная комбинация выпуклых функций на выпуклом множестве с неотрицательными коефициентами  есть выпуклая функция.

 - выпуклая функция. - тоже выпуклая функция.

Если среди выпуклых на функций имеется хоть одна строго выпуклая функция, то линейная комбинация, в которую она входит, будет строго выпуклой.

Условие нахождения минимума выпуклой функции.

Теорема 1

Если функция  выпукла на множестве , то в любой точке локального минимума функция  достигает своего наименьшего значения. Тоесть точек  модет быть много, но значение функции в этих точках одно и то же.

Теорема 2

Наименьшее значение (глобальный минимум) строго выпуклой функции на выпуклом множестве  достигается только в единственной точке.

Теорема 3

Пусть функция  выпукла на выпуклом множестве . Для того, чтобы точка была точкой локального минимума   необходимо и достаточно, чтобы скалярное произведение

Критерий сильной выпуклости для дифференцируемых функций.

Теорема

Для того, чтобы функция  , дифференцируема на выпуклом множестве , была сильно выпуклой, необходимо и достаточно, чтобы существовало некоторое , для которого: