Наступне невикреслене число 5 — просте.
Викреслимо всі числа кратні 5 (кожне п’яте, починаючи з ![]() ). І
т. д.
). І
т. д.
Необхідно викреслити кратні для всіх
простих чисел ![]() , для яких
, для яких ![]() . В результаті всі складені
числа
будуть викреслені, а залишаться всі прості числа. Для
. В результаті всі складені
числа
будуть викреслені, а залишаться всі прості числа. Для ![]() вже після
викреслювання кратних числу 3 всі складені числа виявляються викресленими.
вже після
викреслювання кратних числу 3 всі складені числа виявляються викресленими.
3.
НОД, НОК, Расширенный алгоритм Эвклида. Доказательство.
Розглянемо питання про подільність чисел у множині Z.
Визначення. Якщо для чисел
a, bÎZ у кільці цілих чисел Z існує таке число q,
що a=b´q, то говорять, що a ділиться на b
або b ділить a. Для позначення того факту, що b ділить
а, записують ![]() .
.
Якщо для чисел ![]() виконується
рівність
виконується
рівність![]() , то число a називають кратним
чисел b та q, а самі числа b і q – дільниками
числа a, тобто
, то число a називають кратним
чисел b та q, а самі числа b і q – дільниками
числа a, тобто ![]() та
та ![]() .
.
Розглянемо деякі властивості подільності цілих чисел, що випливають із визначення цілих чисел.
1 Якщо "aÎZ,
то ![]() .
.
2 Для "aÎZ
якщо ![]() , то a= ±1.
, то a= ±1.
3 Для ![]() якщо
якщо ![]() , то
, то ![]() та
та
![]() .
.
4 Для "a,
bÎZ якщо ![]() і
і ![]() ,
то a= ±b.
,
то a= ±b.
5 Для "a,
b, cÎZ якщо ![]() й
й ![]() ,
то
,
то ![]() .
.
6 Для "a,
b, cÎZ якщо ![]() й
й ![]() ,
то
,
то ![]() .
.
7 Для "a,
b, cÎZ якщо ![]() , то (a´c)
, то (a´c)![]() b
b
Важливу роль у теорії подільності відіграє така теорема.
Теорема 1 (про ділення з остачею). Якщо a, bÎZ та b>0, то завжди можна підібрати таку пару цілих чисел q та r, при яких виконується рівність a=b´q+r, де 0£r<b. При цьому числа q та r визначаються однозначно.
За теоремою 1 можна стверджувати, що ціле число a тоді і тільки тоді кратне цілому числу b¹0, коли остача r від ділення a на b дорівнює нулю.
Визначення. Ціле число ![]() називається спільним дільником
цілих чисел
називається спільним дільником
цілих чисел ![]() , якщо кожне із цих чисел
ділитися на
, якщо кожне із цих чисел
ділитися на ![]() .
.
Наприклад, для чисел 12, 18, 21, 36 спільний дільник ![]() =3.
=3.
Визначення. Ціле число d
називається найбільшим спільним дільником (НСД)
чисел ![]() , якщо d – спільний
дільник чисел
, якщо d – спільний
дільник чисел ![]() , що ділиться на
будь-який спільний дільник цих чисел.
, що ділиться на
будь-який спільний дільник цих чисел.
Наприклад, для чисел 12, 18, 36 спільними дільниками будуть числа 2, 3, 6, а НСД d =6.
Теорема 2 НСД чисел ![]() визначається однозначно з точністю до
знака. Інакше, якщо
визначається однозначно з точністю до
знака. Інакше, якщо ![]() та
та ![]() найбільші спільні дільники чисел
найбільші спільні дільники чисел ![]() , то
, то ![]() .
.
1.2 Алгоритм Евкліда
Досить простою процедурою пошуку НСД є алгоритм Евкліда.
Нехай дані два числа a, bÎZ, причому 0<b<a. Необхідно визначити НСД. Для цього
ділять a на b. Якщо b![]() a, то найбільшим спільним дільником є число b. Якщо a не
ділиться на b націло, то одержують частку
a, то найбільшим спільним дільником є число b. Якщо a не
ділиться на b націло, то одержують частку ![]() та залишок
та залишок ![]() ,
причому 0£
,
причому 0£![]() <b. Далі ділять b на
<b. Далі ділять b на ![]() , одержують частку
, одержують частку ![]() і залишок
і залишок ![]() ,
причому 0£
,
причому 0£![]() <
<![]() .
Далі аналогічно ділять
.
Далі аналогічно ділять ![]() на
на ![]() , при цьому одержують частку
, при цьому одержують частку ![]() і залишок
і залишок ![]() ,
причому 0£
,
причому 0£![]() <
<![]() .
І так далі. Цей процес закінчується в тому випадку, коли залишок від ділення
буде дорівнювати нулю, тобто процес ділення є кінцевим, оскільки залишки
.
І так далі. Цей процес закінчується в тому випадку, коли залишок від ділення
буде дорівнювати нулю, тобто процес ділення є кінцевим, оскільки залишки ![]() ,
, ![]() ,
,
![]() ,…, будучи натуральними числами,
зменшуються. Останній залишок, що не дорівнює нулю, є найбільшим спільним
дільником чисел a та b.
,…, будучи натуральними числами,
зменшуються. Останній залишок, що не дорівнює нулю, є найбільшим спільним
дільником чисел a та b.
Алгоритм Евкліда можна сформулювати у вигляді теореми.
Теорема 3 Якщо
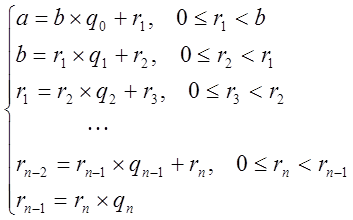 ,
,
то НСД(a, b)=![]() .
.
Наприклад, щоб знайти НСД (2585, 7975) виконаємо такі дії:
7975=2585´3+220, ![]() ,
,
2585=220´11+165, ![]() ,
,
220=165´1+55, ![]() ,
,
165=55´3.
Відповідно до теореми 3 НСД(2585, 7975) =55.
В алгоритмі Евкліда розгляд можна обмежити тільки додатними числами, тому що НСД(a,b)=НСД(|a|, |b|).
procedure Euclid (a,b: integer; var nsd);
var r:integer;
begin
a:=abs(a);
b:=abs(b);
r:=a mod b;
if r=0
then
nsd:=b;
else
while r<>0 do
begin
a:=b;
b:=r;
nsd:=r;
r:=a mod b;
end;
end;
Для знаходження НСД декількох чисел ![]() спочатку знаходять
спочатку знаходять
![]() ,
,
потім
![]() ,
,
…,
![]() .
.
У результаті одержимо ![]() .
.
Теорема 4 Якщо ![]() , то існують такі числа x, yÎZ, що
, то існують такі числа x, yÎZ, що
![]() . (1.1)
. (1.1)
Рівність (1.1) називають лінійним поданням найбільшого спільного дільника чисел a та b.
4.
Функция Эйлера
Важливу роль у теорії чисел відіграє функція Ейлера.
Визначення. Функцією Ейлера ![]() називається
функція, що визначає для кожного числа nÎN
кількість цілих невід’ємних чисел менших n і взаємно простих з n.
називається
функція, що визначає для кожного числа nÎN
кількість цілих невід’ємних чисел менших n і взаємно простих з n.
Властивості функції Ейлера:
1 Функція ![]() мультиплікативна, тобто
для
мультиплікативна, тобто
для ![]() функція
функція ![]() і
для будь-яких взаємно простих чисел m, n (m, nÎN) справедлива рівність
і
для будь-яких взаємно простих чисел m, n (m, nÎN) справедлива рівність
![]() .
.
2 Якщо p – просте число та ![]() ,
то
,
то
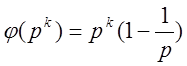 .
.
3 Якщо канонічне розкладання числа nÎN має вигляд
![]() ,
,
то
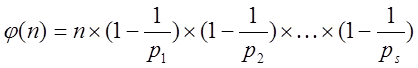 .
.
Наприклад,
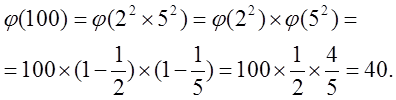
4
Сума значень функції Ейлера для всіх дільників ![]() числа n дорівнює n, тобто
числа n дорівнює n, тобто
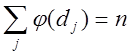 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.