Другие предметы \ Криптология

Модульная арифметика, основные свойства. Понятие простого числа, алгоритмы нахождения. Решето Эратосфена. НОД, НОК. Расширенный алгоритм Эвклида. Функция Эйлера

Страницы работы

6 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

1. Модульная арифметика, основные свойства.

Визначення. Два числа називаються порівнянними за модулем m (mÎN, m¹1), якщо. Це записують так:

Теорема 6 Два числа порівнянні за модулем m тоді і тільки тоді, коли вони при діленні на m мають однакові залишки.

Доведення. Припустимо, залишки від ділення a та b на m рівні r (0£r<m). Покажемо, що . Розділимо a на m та b на m з остачею. Одержимо

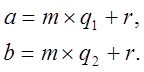
Віднімемо почленно

, ÎZ.

Звідси випливає, що . А значить .

Відзначимо найбільш часто використовувані факти.

Якщо , то, а це значить, що , тобто будь-яке число, кратне m порівняно з нулем за модулем m.

Якщо , де 0£r<m, то . Таким чином, завжди порівняно з залишком r, що отримано при діленні a на m.

Часто залишок r називають відрахуванням.

Розглянемо деякі властивості порівнянь.

Властивості порівнянь, що не залежать від модуля m.

1 Відношення є відношенням еквівалентності, тобто задовольняє вимоги:

– рефлексивності: ;

– симетричності: ;

– транзитивності: .

2 Якщо та , то

3 Якщо і , то

Властивості порівнянь, що залежать від модуля m

4 Якщо і , то

або .

5 Обидві частини порівняння можна розділити на їх спільний дільник d, якщо НСД (d, m)=1.

6 Якщо , то, де .

7 Якщо і НСД(k, m)=d, то

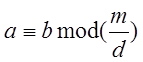8 Якщо , то НСД(a,m)=НСД(b,m).

2. Понятие простого числа, алгоритмы нахождения. Решето Эратосфена

Визначення. Якщо НСД(a,b)=1, то такі числа називаються взаємно простими числами.

Наприклад, числа 21 і 25 є взаємно простими числами, оскільки НСД(21, 25)=1.

Визначення. Якщо НСД()=1, то такі числа називаються попарно взаємно простими числами або взаємно простими.

Розглянемо кілька властивостей взаємно простих чисел.

Для "a, b, cÎZ:

1 Якщо два числа a та b взаємно прості, та , то числа та – взаємно прості.

2 Частки від ділення чисел a та b на їх найбільший спільний дільник d – взаємно прості

НСД .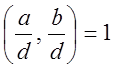

3 Якщо і НСД, то .

4 Якщо НСД(a, b)=1, то число тоді й тільки тоді, коли bс и aс.

5 Якщо НСД(a, c)=1 і НСД(b, c)=1, то НСД(, c)=1.

Розглянемо цілі додатні числа.

Число 1 має тільки один дільник, а саме 1. Кожне натуральне число a, відмінне від 1, має принаймні два дільники – 1 і саме число a.

Визначення. Відмінне від одиниці натуральне число a називається простим, якщо його дільниками є 1 і саме число a. Число a називається складеним, якщо воно має дільники, відмінні від 1 і самого числа a.

Слід зазначити, що число 1 не належить ні до простих, ні до складених чисел.

Розглянемо деякі властивості простих і складених чисел:

1 Будь-яке натуральне число або ділиться на дане просте число, або взаємно просте з ним .

2 Якщо добуток декількох натуральних чисел ділиться на просте число p, то принаймні один із співмножників ділиться на це просте число p.

3 Найменший дільник p () натурального числа n є число просте.

4 Найменший відмінний від 1 дільник складеного числа a не більший ніж .

Теорема 5 Кожне відмінне від 1 натуральне число єдиним способом розкладається на прості множники.

Може виявитися, що в розкладанні числа aÎN на прості множники будуть однакові числа, тому якщо скористатися поняттям ступеня, то число можна записати так:

, (1.2)

де – прості числа, і кожне >0 (i=1, 2,…, s)...

Рівність (1.2) називається канонічною формою розкладання натурального числа a.

Решето́ Ератосфе́на в математиці — простий стародавній алгоритм знаходження всіх простих чисел менших деякого цілого числа , що був створений давньогрецьким математиком Ератосфеном. Він є попередником сучасного решета Аткіна, швидшого, але і складнішого алгоритму.

Метод

Якщо потрібно знайти всі прості числа менші за певне число N, виписуються всі числа від 1 до N² -1. Потім в цьому ряду викреслюються всі числа, які діляться на 2,3, 4 і так далі до N. Числа, які залишилися невикресленими після цієї процедури - прості.

Приклад для