Верифікація програм. Семантики мов програмування, страница 4

Послідовність операторів. Нехай S1  і  S2 – сусідні оператори програми з наступними передумовами і постумовами:

{P1} S1 {P2},        {P2} S2 {P3}.

Правило виведення для цієї послідовності буде

.

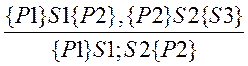Приклад 7.3  Нехай S1 і  S2 є операторами присвоювання:

y:= 3 * x +1,

x:= y +3,

{x<10}.

Передумова другого оператора {y<7} , а першого  –  {x<2}.

Умовний оператор. Правило логічного виведення для умовного оператора

.

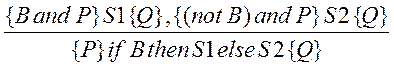Приклад 7.4     if x>0 then y:=y -1 else y:=y+1 .

Постумовою  оператора є {y>0} .

У разі вибору then використовуємо аксіому присвоювання y:=y -1.

Це дає  передумову    { y >1 }.

У разі вибору  else використовуємо  y:=y+1.

Це дає   {y>-1}, таким чином, передумова має вигляд  {y>1} or {y>-1}, але оскільки {y>1} → {y>-1}, можна записати коротше:  {y>-1}.

Цикл з передумовою (while)

У методі індукції існує поняття «індуктивне припущення».

Аналогічну роль у нашому доведені буде відігравати твердження, назване «інваріантом циклу». На його істинність  не повинне впливати виконання операторів циклу, тому він і називається інваріантом.

Аксіоматичний опис циклу while:

 {P} while B do S {Q}.

Правило логічного виведення для обчислення предумови циклу while виглядає так:

,

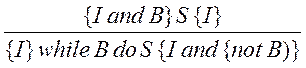де I – інваріант циклу.

Інваріант циклу повинний задовольняти декілька умов.

По-перше, з найслабшої передумови повинна випливати істинність I, по-друге, з істинності I  повинна випливати істинність постумови. Оператори циклу не повинні впливати на інваріант, а цикл повинен закінчуватися.

Основні умови у символьному вигляді:

P → I,

{I and B} S {I},

(I and not B) →Q.

Приклад 7.5      while y < > x then y:=y+1; {y=x}

Для знаходження інваріанта обчислимо ряд передумов для декількох повторень, щоб знайти закономірність.

Для 0 повторень                 {y=x},

для 1 повторення                {y=x-1},

для 2 повторень                  {y=x-2}.

Таким чином, простежується закономірність {y<=x},  яка і буде інваріантом.

Перевіримо умови:

1)   Р збігається з I ,  отже,  P→ I;

            2)  {I and B} S {I}  відповідає

{(y<=x) and (y < > x)} y:=y+1 {y<=x}.

Виконавши присвоювання, одержимо {y+1<=x}, що рівносильно умові {y<x}. А ця умова випливає саме з {(y<=x) and (y < > x)};

3)        (I and (not B))→Q   відповідає

     {(y<=x) and (not(y < > x))}→{y=x}.

У цьому разі передумова є найслабшою, узагалі ж обчислення інваріанта циклу приводить до передумов, що не завжди є найслабшими.

Приклад 7.6  Обчислення факторіала

{n>=0}

k:=n-1;  fact:=n;

while k < > 0 do begin

         fact := fact * k;

         k:=k-1

end;

{fact = n!}.

Інваріант циклу  –  (fact = (k+1) … n) and (k>=0).

Перевіримо умови.

1  Візьмемо I  за  Р, тоді Р→I .

2  У виразі {I and B} S {I} підвираз {I and B} означає  (fact = (k+1) ... n) and (k>0).

Другий оператор циклу має вигляд      {P} k:=k-1 {I},

для нього P: (fact = k … n) and (k>=1).

Перший оператор циклу має вигляд

{P} fact:= fact*k {(fact = k ... n) and (k>=1)},

для нього  P: (fact = (k+1) ...n) and (k>=1), іншими словами, P збігається з {I and B}.

3 Перевіримо виконання  I and B → Q:

 (fac t= (k+1) … n) and (k >= 0) and (k = 0)   → fact = n! .

Завдання до розділу 7

1 Написати  найслабшу  передумову  для оператора y := 3 * x + 1, якщо його постумовою Q є { y < 10 }.

2 Написати  найслабшу  передумову  для оператора y := x + 5, якщо його постумовою Q є { y=43 }.

3 Написати  найслабшу  передумову  для оператора x := x + 1, якщо його постумовою Q є { x ≤ N }.

4 Написати найслабшу передумову для послідовності операторів:

y := 5 * x – 2,

                        x := y – 6,

якщо постумовою Q останнього оператора є { x < 2 }.

5 Написати найслабшу передумову для послідовності операторів:

y := 4 * x – 5,

                        x :=2 * y – 11,

якщо постумовою Q останнього оператора є { x > 3 }.

6 Написати найслабшу передумову для послідовності операторів:

y := 2 * x + 1,

                        x := y – 4,

якщо постумовою Q останнього оператора є { x > 3 }.

7 Написати найслабшу передумову для послідовності операторів:

a := 3 * (2 * b + a),

                        b := 2 * a - 1,

якщо постумовою Q останнього оператора є { b>5 }.

8 Написати найслабшу передумову для умовного оператора

if x>0 then y:=y -2 else y:=y+3 ,

якщо його постумовою Q є { y > 0 }.

9 Написати найслабшу передумову для оператора циклу

     while y < > x then y:=y+5,

якщо його постумовою Q є {y=x}.