Верифікація програм. Семантики мов програмування, страница 2

Денотаційна (математична) семантика. Назва методу походить від слова denote – “означати”. Як і в операційному підході, в основу покладена інтерпретація програми, але вона описується не у термінах машини, а більш традиційними для математики засобами – у термінах деякої сукупності множин, відношень і відображень. Для кожної сутності програми визначаються деякий математичний об’єкт і функція, яка відображає екземпляри цієї сутності в екземпляри цього математичного об’єкта.

Наведемо найпростіший приклад:

<число>::= 0 | … | 9 | < число >0 | | < число >9 .

Денотаційне зображення для цих правил:

M_num(‘0’) = 0;   …;   M_num(‘9’) = 9;

M_num(<число> ‘0’) = 10* M_num(<число >);

M_num(<число>‘1’) = 10* M_num(<число>)+1;

. . .

M_num(<число>‘9’) = 10* M_num(<число>)+9 .

Визначимо VARMAP(i, s) – функцію від імені змінної  і  і стану програми, яка повертає значення змінної i у стані  s.

Вираз для суми:

<вираз>::=<число>|<змінна>|<вираз>’+’<вираз>

Денотаційне зображення цього правила:

M_e(<вираз>, s> =

= case  <вираз>  of

<число>:  M_num(<число>);

<змінна>:   if VARMAP(<змінна >, s)=undef

            then error

            else VARMAP(<змінна >, s);

            <вираз1>’+’<вираз2>:

if M_e(<вираз1>, s))=undef  OR

   M_e(<вираз2>, s))=undef

then error

else M_e(<вираз1>,s) + M_e(<вираз1>,s).

Основи денотаційної семантики були закладені Скоттом. Теорія обчислень Скотта ґрунтується на понятті домена. Домен неформально можна розуміти як деякий аналог множини, який адекватно реалізує рекурсивно визначені функції і множини.

Наведемо способи конструювання нових доменів на основі існуючих.

Функціональний простір. Під функціональним простором з домену D₁ у домен D₂ будемо розуміти домен [D₁→D₂],  який містить всі можливі функції з областю визначення  D₁ і областю значень D₂ :

 [D₁→D₂] = {f | f : D₁→D₂}.

 Декартів добуток – це домен всіх можливих n-к вигляду

[D₁  D₂  …  D_n] =

={(d₁  d₂  …  d_n) | d₁ D₁; d₂ D₂; …; d_n D_n}.

Послідовність. Під   послідовністю    D*    будемо    розуміти   домен    всіх можливих    скінченних послідовностей вигляду d = (d₁,d₂, ..., d_n) з елементів d₁,d₂, ..., d_n домену  D, де n>0.

Диз’юнктна  сума. Під    диз’юнктною    сумою    будемо    розуміти    домен    з    визначенням

[ D₁ +D₂+...+Dn ] ={ (d_i, i) |  d_i,  D_i, 1≤<i ≤ n },

де належність елементів d_i компонентам D_i  однозначно установлюється спеціальними функціями належності.

            Денотаційний підхід найбільш ефективний для функціональних мов програмування.

7.2  Правила  Хоара  і  верифікація

Введемо спочатку поняття часткової і повної коректностіей програм.

Програма Prog частково коректна відносно передумови  P і постумови Q, якщо для будь-якого початкового стану, де виконується  Pі  для якого Prog  завершує свою роботу, у завершальному стані буде виконуватися Q.

Програма Progповністю коректна відносно передумови  P і постумови Q, якщо для будь-якого початкового стану, де виконується  P, правильно, що Prog  завершує свою роботу і в завершальному стані буде виконуватися Q.

Одним з методів верифікації програм є метод індуктивних тверджень Флойда. Розглянемо його на прикладі простої програми обчислення цілої частини квадратного кореня числа x. Блок-схема програми зображена на рис. 7.1.

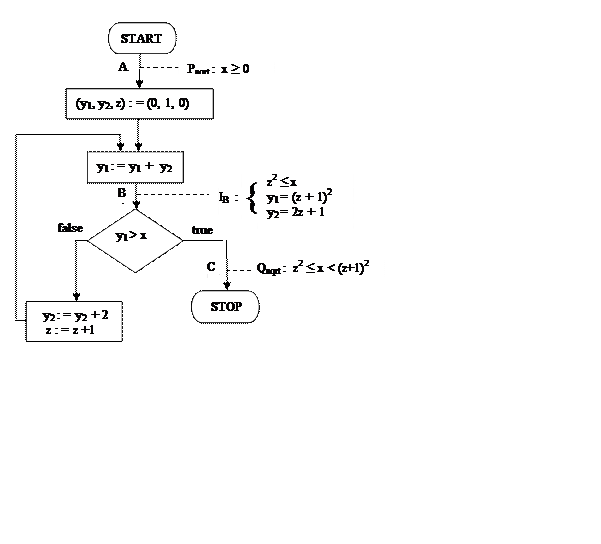
Рисунок 7.1 – Блок-схема програми

Схема доведення складається з трьох кроків.

Крок 1 – контрольні точки. Спочатку на ребрах блок-схеми вибирається множина контрольних точок. Ця множина повинна задовольняти такі умови.

1 Кожний цикл у блок-схемі містить хоча б одну контрольну точку.

2 Ребро, яке виходить з початкового оператора, має контрольну точку. Вона називається початковою точкою.

3 Для кожного завершального оператора ребро, яке веде до нього, має контрольну точку. Вона називається завершальною точкою.

На нашій блок-схемі такими точками є A, B і C.

Базовим шляхом називається такий шлях у блок-схемі, на кінцях якого знаходяться контрольні точки, і він не містить проміжних точок.

Для нашої блок-схеми базовими є такі шляхи:

1  Шлях α з точки  A у точку  B через оператори (y₁,y₂, z) := (0, 1, 0)   і   y₁ : = y₁  +  y₂ .

2  Шлях β з точки  B у точку  B  через оператори y₁>x ,  y₂ := y₂  + 2 ,   z : = z +1  і  y₁ : = y₁  +  y₂ .

3  Шлях γ з точки  B у точку  C  через оператор  y₁>x .

Крок 2 – індуктивні твердження. На цьому кроці для кожної контрольної точки  S  вибирається формула I_{S .} Вона називається індуктивним твердженням для S. Індуктивне твердження  I_S  повинне бути інваріантом в S для передумови P. На наступному третьому кроці методу Флойда цей факт доводиться для всіх індуктивних тверджень.