Алгоритм навчання Хебба. Алгоритм навчання Кохонена. Алгоритм навчання процедурою зворотного поширення помилки, страница 2

Оцінка реакції прихованих нейронів виробляється обчисленням зваженого значення помилки, знайденої для шару ефекторів. За вагову функцію використовують поточні значення ваги проекційних зв’язків, які йдуть від прихованих нейронів до ефекторів. Помилка немовби поширюється в зворотному діючому ззовні стимулу напрямку. Якщо прихованих шарів декілька перелік помилок наводять для кожного, починаючи з шару ефекторів.

Цільовою функцією помилки ШНМ, що мінімізується, є величина:

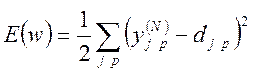                                                                    ,     (4.1)

де  - реальний вихідний стан нейрона j вихідного шару N ШНМ при подачі на її входи р-ого образу;  - ідеальний (цільовий) стан цього нейрона.

Підсумок ведеться за всіма нейронами вихідного шару і за всіма оброблюваними ШНМ образами. Мінімізація здійснюється за методом градієнтного спуску, тобто ваги модифікуються таким чином:

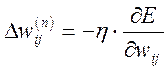                                                                           ,             (4.2)

де - ваговий коефіцієнт синапсу, що з’єднує і тий нейрон шару п-1 з j-тим нейроном шару п, η –коефіцієнт швидкості навчання (0<η<1). Похідну з (4.2) можна подати у вигляді:

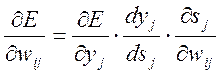                                                                       ,        (4.3)

де - вихідний сигнал нейрона j,  - зважена сума його вхідних сигналів (аргумент активаційної функції).

Очевидно, =.

 вказує на те, що похідна активаційної функції за її аргументом повинна бути визначена по всій осі абсцис. (Наприклад, якщо за активаційну функцію взяти гіперболічний тангенс, то =1-s²).

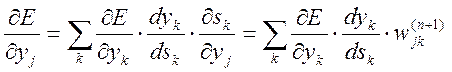                                                ,                                                                                      (4.4)

Тут підсумовування за k виконується серед нейронів шару (п+1)

Позначимо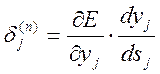, тоді

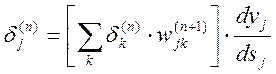                                                                  .    (4.5)

Для вихідного шару N

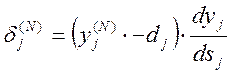                                                                      .       (4.6)

Тоді (4.2) приймає вигляд:

                                                                        .         (4.7)

Повний алгоритм навчання ШМН за процедурою зворотного поширення помилки має вигляд:

a)  Подати на входи ШНМ один з можливих образів в режимі звичайного функціонування мережі.

b)  Розрахувати  для вихідного шару за (4.6).

c)  Розрахувати зміни ваг для вихідного шару за (4.5) та (4.7).

d)  Розрахувати  та  за (4.5) та (4.7) для всіх інших шарів n=N-1..1.

e)  Скоригувати вагу всіх синапсів у ШНМ .

f)  Якщо помилка істота, перейти на а).

ШНМ на кроці 1 поперемінно у випадковому порядку подаються всі тренувальні образи.

МІСТКІСТЬ ШНМ

Місткістю ШНМ називають кількість образів, запропонованих на її входи, які вона спроможна розпізнати.

У мережі Хопфілда кількість запам’ятованих образів не може перевищувати 14% від кількості нейронів. При наближенні до цієї межі з’являються неправдиві атрактори, що перешкоджають конвергенції до запам’ятованих станів. Можлива втрата стаціонарності.

Для ШНМ із двома шарами (вихідним та прихованим) детермінована місткість C_d оцінюється так:

,

де  - кількість ваг, що повлаштовуються,  - кількість нейронів у вихідному шарі. При чому дана оцінка використовується для мереж, де кількість входів  і нейронів у прихованому шарі  задовольняє нерівностям:

+>,

/>1000.

Проте, дана оцінка використовувалась для ШНМ з активаційними функціями у вигляді порога, а місткість ШМН зі гладкими функціями значно більша. Те, що дана оцінка детермінована, вказує на можливість її використання абсолютно для всіх можливих вхідних образів, які можуть бути подані  входами. Насправді розподіл вхідних образів, як правило, має певну регулярність, що дозволяє ШМН робити узагальнення і таким чином збільшувати реальну місткість. Якщо розподіл невідомий, то говорити про реальну місткість можна тільки приблизно, але вона разів у два може перевищувати детерміновану.

Для ШМН, де більше двох шарів, місткість залишається відкритою.

Необхідна потужность вихідного шару ШНМ, що виконує остаточну класифікацію образів, розраховується з кількості класів образів. Наприклад, для двох класів достатньо одного виходу (при цьому кожний логічний рівень 1 або 0 позначатиме окремий клас), для 4 класів достаньмо 2 виходи и т.д.

Проте надійність результатів роботи такої ШНМ не дуже велика. Для її підвищення бажано ввести надмірність виділення кожному класу одного нейрона у вихідному шарі або, ще краще, декількох, кожний з яких навчається визначати приналежність образу до класу зі своїм ступенем достовірності. Такі ШНМ дозволяють класифікувати вхідні образи, об’єднані у нечіткі (розмиті або такі, що перетинаються) множини. Ця властивість наближає ШМН до умов реального життя.