





ЛЕКЦІЯ 4
Складність розв’язання систем рівнянь.
План
1. Метод Гауса і оцінка його складності.
2. LUR – розкладання матриць.
3. Метод І.В. Коновальцева і оцінка складності.
Метод Гауса і оцінка його складності.
Ми розглянемо алгоритми розв’язку систем лінійних
рівнянь над полем ![]() , що
складається з двох елементів.
, що
складається з двох елементів.
Нехай система лінійних рівнянь над полем ![]() має вигляд:
має вигляд:
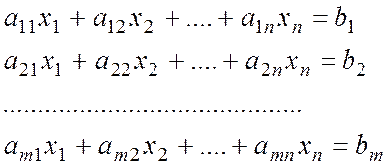
![]()
Припустимо,
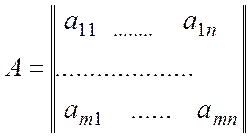 ,
, 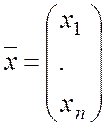 ,
,
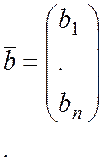 .
.
Тоді система, яку ми розглядаємо приймає
вигляд ![]() .
.
Метод Гауса.
Як відомо з курсу лінійної алгебри, даний
метод базується на послідовному виключенні невідомих рівнянь з системи. В
термінах матриць виключення невідомих еквівалентне виконанню операції додавання
в полі ![]() рядків матриці
рядків матриці ![]() . Наприклад, нехай перші два
рівняння системи мають вигляд:
. Наприклад, нехай перші два
рівняння системи мають вигляд:
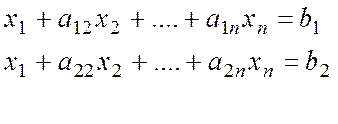
Виражаючи ![]() з першого рівняння ( операція + в полі
з першого рівняння ( операція + в полі ![]() ), і, підставляючи його в друге рівняння, отримуємо
), і, підставляючи його в друге рівняння, отримуємо
![]() ,
,
виключивши таким
чином невідоме ![]() . Таке перетворення
відповідає заміні в матриці
. Таке перетворення
відповідає заміні в матриці
![]()
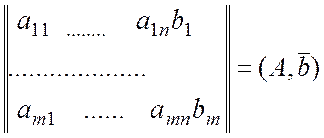
другого рядка на суму першого і другого.
Визначимо наступні елементарні операції перетворення над матрицями:
1) додавання одного рядку матриці до іншого
2) перестановка рядків матриці;
3) перестановка стовпців.
Зауважимо, що за
перестановки рядків матриці ![]() система
рівнянь не зміниться, а за перестановки стовпців матриці
система
рівнянь не зміниться, а за перестановки стовпців матриці ![]() станеться перенумерація
невідомих.
станеться перенумерація
невідомих.
Як відомо,
метод Гауса полягає в наступному. На першому кроці матриця ![]() перетворюється на матрицю
перетворюється на матрицю ![]() , у якої перший
стовпчик співпадає з першим стовпчиком одиничної матриці. Для цього треба
знайти рядок, у якому перший елемент рівний одиниці (якщо такого нема, слід
переставити стовпчики і додати його до інших рядків, що містять одиницю в
першому стовпці, на другому кроці виконується те ж перетворення над підматрицею
матриці
, у якої перший
стовпчик співпадає з першим стовпчиком одиничної матриці. Для цього треба
знайти рядок, у якому перший елемент рівний одиниці (якщо такого нема, слід
переставити стовпчики і додати його до інших рядків, що містять одиницю в
першому стовпці, на другому кроці виконується те ж перетворення над підматрицею
матриці ![]() , отриманої
видаленням першого рядка і першого стовпця. Продовжуючи цей процес, матрицю
приводять до вигляду:
, отриманої
видаленням першого рядка і першого стовпця. Продовжуючи цей процес, матрицю
приводять до вигляду:
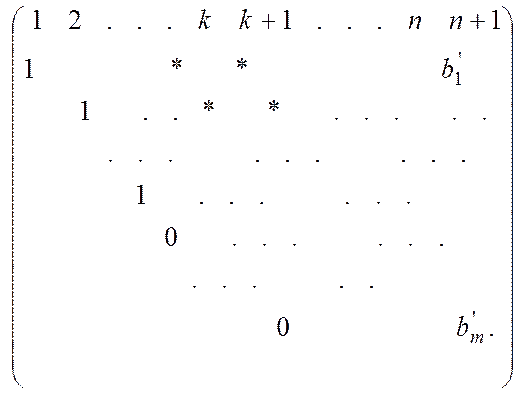
Тепер система
рівнянь ![]() має ту ж множину
роз’язків, що і початкова, можливо зі зміненим порядком
нумерації змінних). Якщо деякі з елементів
має ту ж множину
роз’язків, що і початкова, можливо зі зміненим порядком
нумерації змінних). Якщо деякі з елементів ![]() відмінні від нуля, то система лінійних рівнянь не має розв’язків. Якщо
відмінні від нуля, то система лінійних рівнянь не має розв’язків. Якщо
![]() , то система має
, то система має ![]() розв’язків. Для їх знаходження фіксують довільним чином змінні
розв’язків. Для їх знаходження фіксують довільним чином змінні ![]() (
(![]() способів ), а потім
знаходять значення змінної
способів ), а потім
знаходять значення змінної ![]() з
з ![]() -го рівняння, значення
-го рівняння, значення ![]() з (
з (![]() )-го рівняння і т. д. Так
знаходять усі рішення початкової системи рівнянь.
)-го рівняння і т. д. Так
знаходять усі рішення початкової системи рівнянь.
Зауважимо, що всі
перетворення не змінюють ранг матриці. Матриця ![]()
має ранг ![]() , якщо
, якщо ![]() має, принаймні, одну
невироджену підматрицю порядку
має, принаймні, одну
невироджену підматрицю порядку ![]() , а всі підматриці
, а всі підматриці ![]() більш високих
порядків вироджені. Квадратна матриця називається невиродженою або виродженою в
залежності від того, чи відмінний її визначник від нуля чи рівний нулю.
більш високих
порядків вироджені. Квадратна матриця називається невиродженою або виродженою в
залежності від того, чи відмінний її визначник від нуля чи рівний нулю.
Приклад:
Підрахуємо
працемісткість методу. На першому кроці виконується не більше ![]() операцій додавання, на
другому – не більше
операцій додавання, на
другому – не більше ![]() і
т.д. Отже, працемісткість перетворення матриці
і
т.д. Отже, працемісткість перетворення матриці ![]() до вигляду
до вигляду ![]()
оцінюється
величиною 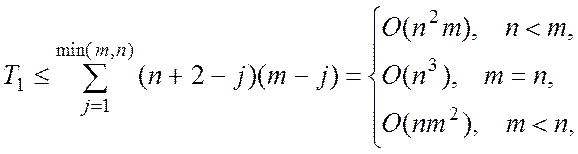
або інакше ![]()
При ![]() дана оцінка приймає
вигляд
дана оцінка приймає
вигляд
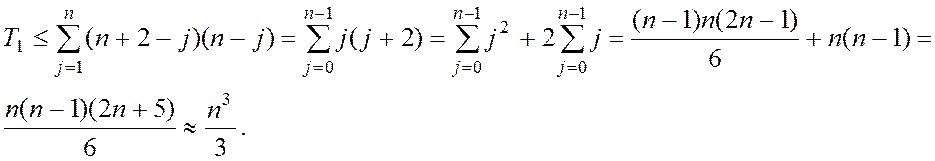
Нескладно
показується, що для знаходження кожного з рішень потрібно не більше ![]()
операцій додавання.
Таким чином, оскільки ![]() , загальна трудомісткість методу
Гауса оцінюється величиною
, загальна трудомісткість методу
Гауса оцінюється величиною ![]() .
.
LUR - розкладання матриць.
Якщо доводиться вирішувати не одну систему лінійних рівнянь, а багато таких систем з однаковою лівою частиною і різними правими частинами, то використовують модифікацію методу Гауса.
Метод Гауса
фактично полягає в приведенні матриці ![]()
за допомогою
елементарних операцій до верхньотрикутного вигляду. Кожна з елементарних
операцій еквівалентна множенню матриці ![]() на деяку матрицю:
на деяку матрицю:
1) при ![]() збільшення
збільшення
![]() -го рядка до
-го рядка до ![]() -
го здійснюється множенням зліва на матрицю
-
го здійснюється множенням зліва на матрицю 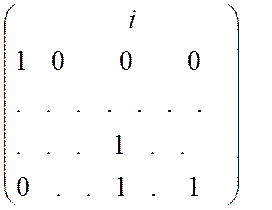 =
=![]()
розміру ![]() ; ;
; ;
2) перестановка ![]() -го і
-го і ![]() -го
рядків
-го
рядків ![]() еквівалентно множенню зліва на матрицю
еквівалентно множенню зліва на матрицю
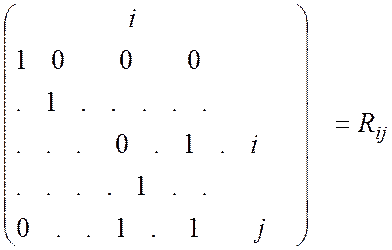
розміру ![]() .
.
3) перестановка
- го і - го стовпця еквівалентна множенню справа на матрицю ![]() розміру
розміру
![]() .
.
Виділимо особливий випадок, коли можна обмежитися виконанням тільки елементарних операцій першого типа.
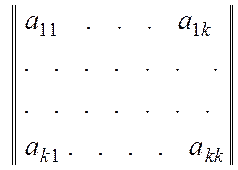 =
=![]()
головний мінор матриці
![]() .
.
Справедливі наступні теореми.
Теорема.
Якщо весь головний
мінор матриці ![]() відмінний від нуля, то досить використовувати
тільки операції першого типа.
відмінний від нуля, то досить використовувати
тільки операції першого типа.
Теорема.
Для будь-якої матриці
![]() розміру
з ненульовим головним мінором знайдуться невироджені ніжнетреугольная матриця
розміру і верхнетреугольная матриця розміру такі, що .
розміру
з ненульовим головним мінором знайдуться невироджені ніжнетреугольная матриця
розміру і верхнетреугольная матриця розміру такі, що .
Теорема.
Невироджену матрицю
розміру ![]() можна перестановкою тільки рядків
можна перестановкою тільки рядків
( або тільки стовпців
) перевести в матрицю, у якої весь головний мінор відмінний від нуля.
Нагадаємо, що, якщо ![]() - визначник порядку
- визначник порядку ![]() ,
то мінором
,
то мінором ![]() елементу
елементу ![]() називають визначник
порядку
називають визначник
порядку ![]() , що виходить з
, що виходить з ![]() викреслюванням
викреслюванням ![]() -го рядка і
-го рядка і ![]() - го
стовпця.
- го
стовпця.
Як слідство з цих
теорем можна одержати твердження: всяку невироджену
матрицю ![]() можна привести до вигляду
можна привести до вигляду![]() ,
де
,
де ![]() -
підстановлювальні матриці, а
-
підстановлювальні матриці, а ![]() і
і ![]() , відповідно, нижні і верхні трикутні матриці.
На підставі цього твердження доводиться, що розкладання матриці
, відповідно, нижні і верхні трикутні матриці.
На підставі цього твердження доводиться, що розкладання матриці![]() ,
вказане вище, знаходиться за
,
вказане вище, знаходиться за ![]() операцій, а після того, як
воно знайдене, рішення кожної системи ( з своєю правою частиною) знаходиться за
операцій, а після того, як
воно знайдене, рішення кожної системи ( з своєю правою частиною) знаходиться за
![]() операцій.
операцій.
Метод І.В. Коновальцева.
Отже, завдання полягає в знаходженні рішення систем лінійних рівнянь
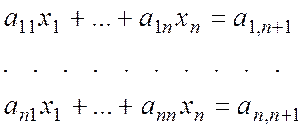
у разі, коли елементи
матриці ![]() даної системи належать кінцевому полю з
даної системи належать кінцевому полю з ![]() елементів. Алгоритм Коновальцева полягає в
наступному.
елементів. Алгоритм Коновальцева полягає в
наступному.
Перші ![]() елементів
елементів ![]() -го рядку
матриці
-го рядку
матриці ![]() назвемо кортежем
назвемо кортежем ![]() .
.
Перебираючи
послідовно рядки матриці ![]() , знаходять перший кортеж
, знаходять перший кортеж ![]() ,
відмінний від
,
відмінний від ![]() , і ставлять його на перше місце. У одержаній
матриці порівнюють кортеж
, і ставлять його на перше місце. У одержаній
матриці порівнюють кортеж ![]() з кортежем
з кортежем ![]() .
Якщо
.
Якщо ![]() ,
то віднімають з другого рядка перший, після чого кортеж другого рядка стане
нульовим. Якщо
,
то віднімають з другого рядка перший, після чого кортеж другого рядка стане
нульовим. Якщо![]() , то порівнюють
, то порівнюють ![]() з
з ![]() і поступають аналогічно попередньому. На
останньому етапі порівнюють кортежі
і поступають аналогічно попередньому. На
останньому етапі порівнюють кортежі ![]() і
і ![]() і виконують відповідні операції. Відзначимо,
що в одержаній матриці кортеж
і виконують відповідні операції. Відзначимо,
що в одержаній матриці кортеж ![]() і серед кортежів
і серед кортежів ![]() немає
рівних
немає
рівних ![]() . Розглядають рядки 2,…,
. Розглядають рядки 2,…,![]() , одержаної матриці, знаходять перший ненульовий
кортеж, міняють його місцями з кортежем
, одержаної матриці, знаходять перший ненульовий
кортеж, міняють його місцями з кортежем ![]() (переставляючи
відповідні рядки ) і повторюють процедуру, описану вище. Якщо число різних
ненульових кортежів дорівнює
(переставляючи
відповідні рядки ) і повторюють процедуру, описану вище. Якщо число різних
ненульових кортежів дорівнює ![]() , то після
, то після ![]() кроків
матриця
кроків
матриця ![]() системи лінійних рівнянь приймає вигляд
системи лінійних рівнянь приймає вигляд
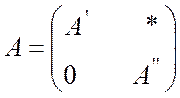 ,
,
де матриця ![]() має
має
![]() рядків і
рядків і ![]() стовпців. Алгоритмом Гауса
приводять матрицю
стовпців. Алгоритмом Гауса
приводять матрицю ![]() до верхньотрикутного
вигляду. У разі, коли визначник матриці
до верхньотрикутного
вигляду. У разі, коли визначник матриці ![]() відмінний від
нуля, одержана матриця приймає вигляд
відмінний від
нуля, одержана матриця приймає вигляд
 .
.
Якщо ж на цьому етапі
з'ясовується, що![]() , то процес закінчується. Цей
етап застосовується
, то процес закінчується. Цей
етап застосовується ![]() разів, де
разів, де ![]() вибирається виходячи з умов
вибирається виходячи з умов
![]() ,
,
але
![]() .
.
В результаті матриця ![]() приймає вигляд
приймає вигляд
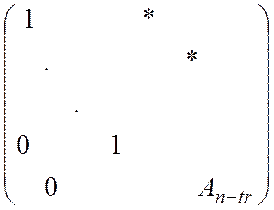 .
.
Перетворення
підматриці ![]() до трикутного вигляду здійснюється методом
Гауса. В результаті матриця
до трикутного вигляду здійснюється методом
Гауса. В результаті матриця ![]() перетвориться в
матрицю трикутного вигляду з одиничними елементами на головній діагоналі. (
якщо
перетвориться в
матрицю трикутного вигляду з одиничними елементами на головній діагоналі. (
якщо ![]() ). Потім розв'язується система
лінійних рівнянь з трикутною матрицею коефіцієнтів. Доведено, що число всіх
операцій ( арифметичних і допоміжних) не перевершує величини
). Потім розв'язується система
лінійних рівнянь з трикутною матрицею коефіцієнтів. Доведено, що число всіх
операцій ( арифметичних і допоміжних) не перевершує величини
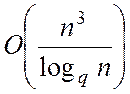 .
.
На закінчення
відзначимо, що для рівнянь з невиродженою матрицею Штрассеном був
запропонований алгоритм зі складністю ![]() операцій.
Але пониження складності в ньому досягнене завдяки використанню пам'яті ЕОМ.
операцій.
Але пониження складності в ньому досягнене завдяки використанню пам'яті ЕОМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.