4 Расчет характеристик КС на основе сетевых стохастических моделей
4.1 Расчет сетевых стохастических моделей
Этапы расчета:
1. построение стохастической сети и
расчет ее параметров ![]() ;
;
2. расчет интенсивностей потоков ![]() и коэффициентов передач
и коэффициентов передач ![]() для подсистем
для подсистем ![]() сети;
сети;
3. определение вероятностей состояний подсистем и системы в целом;
4. расчет характеристик подсистем (![]() ,
, ![]() ,
, ![]() ,
, ![]() );
);
5. расчет общесетевых характеристик (![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
Для нахождения
коэффициентов передач ![]() необходимо рассчитать интенсивности
потоков в подсистемах сети
необходимо рассчитать интенсивности
потоков в подсистемах сети
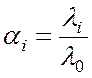 ,
,
где ![]() - входной поток в
- входной поток в ![]() -й
подсистеме,
-й
подсистеме, ![]() - входной поток сети;
- входной поток сети;
При этом поток на входе ![]() -й подсистемы образован суммой потоков от
-й подсистемы образован суммой потоков от ![]() связанных с ней подсистем:
связанных с ней подсистем:
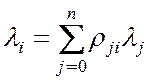 , (
, (![]() ) (4.1)
) (4.1)
Для разомкнутых
стохастических сетей известна интенсивность источника заявок ![]() и поэтому система (4.1) имеет единственное
решение.
и поэтому система (4.1) имеет единственное
решение.
Для замкнутой сети ни
одна из интенсивностей ![]() , …,
, …, ![]() заранее
неизвестна, определитель системы уравнений (4.1) равен нулю и система имеет
бесконечное множество решений. Однако систему (4.1) можно решить подставив
значение
заранее
неизвестна, определитель системы уравнений (4.1) равен нулю и система имеет
бесконечное множество решений. Однако систему (4.1) можно решить подставив
значение ![]() . В этом случае корни
. В этом случае корни ![]() , …,
, …, ![]() численно
определяют значения
численно
определяют значения ![]() , …,
, …, ![]() .
.
4.2 Характеристики разомкнутых стохастических сетей
Загрузка систем в сети определяется в виде
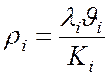 ,
,
где ![]() - интенсивность входного потока заявок,
- интенсивность входного потока заявок, ![]() - длительность обслуживания заявок в
системе
- длительность обслуживания заявок в
системе ![]() ,
, ![]() - общее
число каналов в системе.
- общее
число каналов в системе.
Выражение (4.2) определяет среднее число занятых каналов СМО.
![]() . (4.2)
. (4.2)
Выражение (4.3) характеризует вероятность того, что многоканальная СМО свободна от обслуживания заявок.
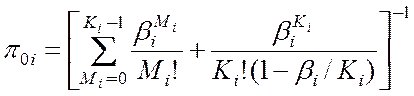 , (4.3)
, (4.3)
где ![]() - количество заявок, находящихся в системе
- количество заявок, находящихся в системе
![]()
Характеристики систем в сети.
Среднее число заявок,
ожидающих обслуживания в системе ![]() , т.е. средняя длина
очереди
, т.е. средняя длина
очереди
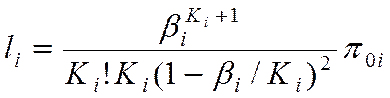 . (4.4)
. (4.4)
Среднее число заявок пребывающих
в системе ![]()
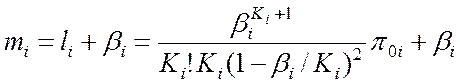 . (4.5)
. (4.5)
Среднее время ожидания заявки в очереди
 . (4.6)
. (4.6)
Среднее время пребывания заявок в системе
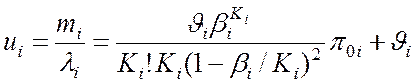 . (4.7)
. (4.7)
Характеристики сети.
Используя (4.4) – (4.7) определяются характеристики в целом.
Среднее число заявок, ожидающих обслуживания в сети,
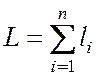 . (4.8)
. (4.8)
Среднее число заявок, пребывающих в сети,
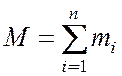 . (4.9)
. (4.9)
Среднее время ожидания заявки в сети
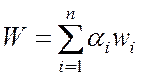 . (4.10)
. (4.10)
Среднее время пребывания заявки в сети
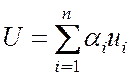 . (4.11)
. (4.11)
4.3 Характеристики замкнутых стохастических сетей
В замкнутой ССМ
циркулирует постоянное ограниченное число заданий ![]() и
условие стационарности в этом случае будет выполняться всегда.
и
условие стационарности в этом случае будет выполняться всегда.
Различные распределения ![]() заявок по системам сети определяют ее
состояния. Состояние (
заявок по системам сети определяют ее
состояния. Состояние (![]() ) означает, что в системе
) означает, что в системе ![]() пребывает
пребывает ![]() заявок
(часть обслуживается и часть ожидает в очереди), в системе
заявок
(часть обслуживается и часть ожидает в очереди), в системе ![]() пребывает
пребывает ![]() заявок и
т.д. Множество таких состояний обозначается как
заявок и
т.д. Множество таких состояний обозначается как ![]() , а
мощность этого множества, т.е. число всевозможных состояний, - через
, а
мощность этого множества, т.е. число всевозможных состояний, - через ![]() . Число различных распределений
. Число различных распределений ![]() заявок по
заявок по ![]() системам
конечно и равно числу сочетаний:
системам
конечно и равно числу сочетаний:
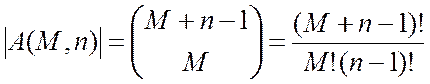 . (4.12)
. (4.12)
Вероятности состояний замкнутой сети определяются следующим образом:
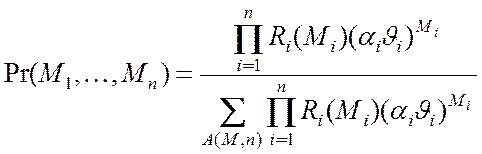 , (4.13)
, (4.13)
где 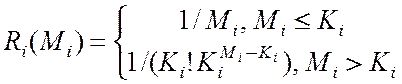 ;
; 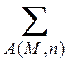 -
символ суммирования по всем состояниям множества
-
символ суммирования по всем состояниям множества ![]() .
.
Загрузка систем замкнутой сети.
Для одноканальных СМО загрузка определяется как
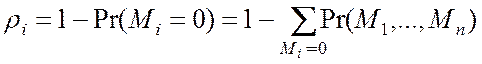 . (4.14)
. (4.14)
Загрузка каждого из
каналов многоканальной системы ![]() определяется как
определяется как
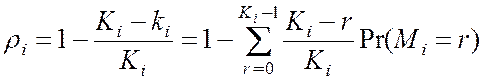 , (4.15)
, (4.15)
где 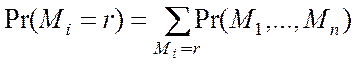 - вероятность того, что в системе
- вероятность того, что в системе ![]() находится точно
находится точно ![]() заявок,
а заявки среди других систем распределяются любыми возможными сочетаниями,
суммирование ведется по всем состояниям множества
заявок,
а заявки среди других систем распределяются любыми возможными сочетаниями,
суммирование ведется по всем состояниям множества ![]() , для
которых число заявок в системе
, для
которых число заявок в системе ![]() равно
равно ![]() .
.
Характеристики систем в сети.
Интенсивность потока, входящего в систему
![]() . (4.16)
. (4.16)
Среднее число заявок,
ожидающих обслуживания в системе ![]() , т.е. средняя длина
очереди
, т.е. средняя длина
очереди
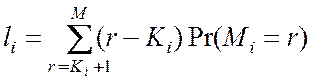 . (4.17)
. (4.17)
Среднее число заявок пребывающих
в системе ![]()
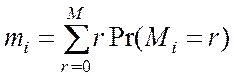 . (4.18)
. (4.18)
Для проверки значений ![]() , вычисленных с помощью (4.18), можно
воспользоваться равенством
, вычисленных с помощью (4.18), можно
воспользоваться равенством ![]() .
.
Среднее время ожидания заявки в очереди
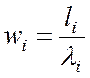 . (4.19)
. (4.19)
Среднее время пребывания заявок в системе
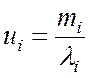 . (4.20)
. (4.20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.