






Практическое занятие № 1
Расчет трудоемкости выполнения алгоритма
1.1 Цель работы
Изучение методов оценки трудоемкости алгоритмов на основе теории марковских цепей и сетевого подхода, а также определение максимального и минимального времени выполнения алгоритма.
1.2 Методические указания по организации самостоятельной работы студентов
При подготовке к практическому занятию необходимо изучить методические указания, соответствующие разделы конспекта лекций и раздел, приведенный в [1, с. 40 - 49].
Трудоемкость алгоритма – количество вычислительной работы, требуемой для реализации алгоритма.
В задачах оценки трудоемкости операторы алгоритма разделяют на функциональные, перехода и ввода-вывода.
Функциональный оператор задает преобразование на множестве данных, т.е. задает некоторую совокупность вычислительных операций. Оператор перехода задает порядок вычисления функциональных операторов и правило выбора одного из возможных путей развития вычислительного процесса, соответствующего текущим значениям данных. Оператор ввода-вывода задает обращение к определенному файлу с целью передачи некоторого количества информации. Функциональные операторы и операторы перехода называют основными операторами.
Совокупность операторов и связей между ними наиболее наглядно представляется графом алгоритма, где вершины соответствуют основным операторам алгоритма, а дуги отображают связи между операторами.
Вершины графа бывают трех типов: начальная, конечная и операторная. Начальная вершина определяет начало алгоритма. Эта вершина не имеет ни одного входа и имеет только один выход. Конечная вершина определяет конец алгоритма и имеет не менее одного входа и ни одного выхода. Операторная вершина соответствует основному оператору или оператору ввода-вывода. Если она представляет функциональный оператор или ввода-вывода, то может иметь не меньше одного входа и только один выход. Если она представляет оператор перехода, то может иметь не меньше одного входа и не меньше двух выходов.
Граф алгоритма является корректным, если выполняются условия:
- имеется только одна начальная и только одна конечная вершина;
- для каждой вершины кроме начальной существует по крайней мере один путь, ведущий в эту вершину из начальной;
- из каждой вершины кроме конечной существует по крайней мере один путь, ведущий из этой вершины в конечную;
- выход из любой вершины должен вести только к одной вершине графа;
- при любых значениях логических условий существует путь из начальной вершины в конечную, причем любому фиксированному набору значений условий соответствует только один такой путь.
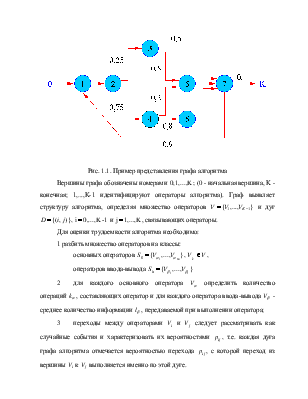
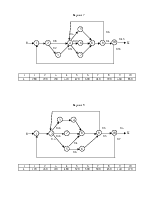
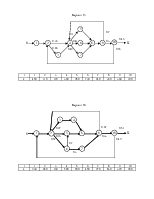
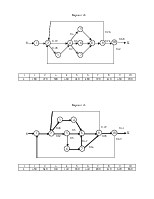
Пример графа алгоритма приведен на рис. 1.1.
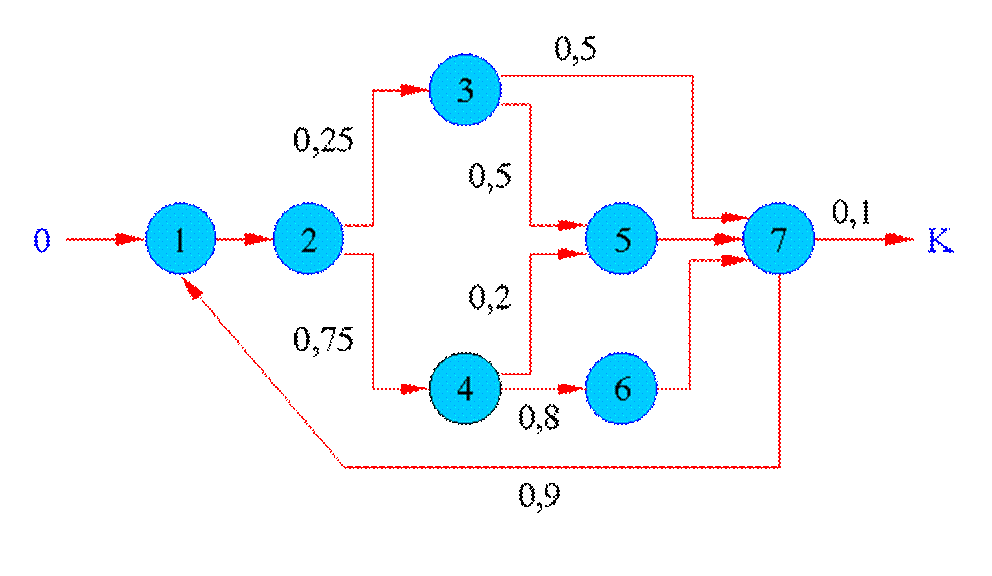
Рис. 1.1. Пример представления графа алгоритма
Вершины графа
обозначены номерами ![]() ; (0 - начальная вершина, K -
конечная; 1,...,K-1 идентифицируют операторы алгоритма). Граф выявляет
структуру алгоритма, определяя множество операторов
; (0 - начальная вершина, K -
конечная; 1,...,K-1 идентифицируют операторы алгоритма). Граф выявляет
структуру алгоритма, определяя множество операторов ![]() и дуг
и дуг ![]() ,
, ![]() и
и ![]() , связывающих операторы.
, связывающих операторы.
Для оценки трудоемкости алгоритма необходимо:
1 разбить множество операторов на классы:
основных операторов ![]() ,
, ![]() ,
,
операторов ввода-вывода ![]()
2
для каждого
основного оператора ![]() определить количество операций
определить количество операций ![]() , составляющих оператор и для каждого
оператора ввода-вывода
, составляющих оператор и для каждого
оператора ввода-вывода ![]() - среднее количество информации
- среднее количество информации ![]() , передаваемой при выполнении оператора;
, передаваемой при выполнении оператора;
3
переходы между
операторами ![]() и
и ![]() следует
рассматривать как случайные события и характеризовать их вероятностями
следует
рассматривать как случайные события и характеризовать их вероятностями ![]() , т.е. каждая дуга графа алгоритма
отмечается вероятностью перехода
, т.е. каждая дуга графа алгоритма
отмечается вероятностью перехода ![]() , с которой переход из
вершины
, с которой переход из
вершины ![]() к
к ![]() выполняется
именно по этой дуге.
выполняется
именно по этой дуге.
Так как
вычислительный процесс не может приостановиться в вершине ![]() , то с вероятностью 1 произойдет переход к
какой-либо вершине графа алгоритма. Поэтому вероятности переходов должны
отвечать условию:
, то с вероятностью 1 произойдет переход к
какой-либо вершине графа алгоритма. Поэтому вероятности переходов должны
отвечать условию:
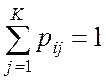 , (
, (![]() ); (1.1)
); (1.1)
Значения ![]() зависят от вероятностей выполнения
условия, проверяемого оператором
зависят от вероятностей выполнения
условия, проверяемого оператором ![]() с целью выбора пути
перехода.
с целью выбора пути
перехода.
Пусть ![]() - среднее число обращений к операторам
- среднее число обращений к операторам ![]() за один прогон алгоритма. Тогда
характеристика трудоемкости может быть вычислена следующим образом:
за один прогон алгоритма. Тогда
характеристика трудоемкости может быть вычислена следующим образом:
среднее число операций, выполняемых при одном прогоне алгоритма
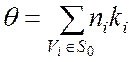 (1.2)
(1.2)
где ![]() - множество
операторных вершин рассматриваемого графа алгоритма;
- множество
операторных вершин рассматриваемого графа алгоритма; ![]() -количество
операций, порождаемых оператором
-количество
операций, порождаемых оператором ![]() .
.
В связи с
тем, что вероятности переходов ![]() постоянны и после
выполнения оператора
постоянны и после
выполнения оператора ![]() (
(![]() ) переход
к следующему оператору определяется только распределением вероятностей
) переход
к следующему оператору определяется только распределением вероятностей ![]() , т.е. не зависит от хода вычислительного
процесса в прошлом, то процесс выполнения алгоритма является марковским
процессом с
, т.е. не зависит от хода вычислительного
процесса в прошлом, то процесс выполнения алгоритма является марковским
процессом с ![]() состояниями
состояниями ![]() ,
соответствующими пребыванию процесса в вершинах
,
соответствующими пребыванию процесса в вершинах ![]() графа
алгоритма.
графа
алгоритма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.