Погрешность косвенных измерений

1.7   Погрешность косвенных измерений.

Как уже отмечалось, косвенные измерения величин выполняются на основе расчётных формул. Например, производится измерения сопротивления однородного участка электрической цепи по измеренным значениям тока I и напряжения U на этом участке. По закону Ома имеем

R =  .Но значения U и I являются достоверными с определённой степенью вероятности и в

определённом доверительном интервале. Поэтому значение  R следует так же рассматривать как случайное событие.

Расчёт погрешности измерения в этом случае выполняется по формуле, которая получается на основе расчётной формулы и правил операций дифференцирования.

Формулу для расчёта величины погрешности можно построить следующим образом: расчётная формула логарифмируется, а затем берётся дифференциал от левой и правой части выражения, после чего оператор d дифференцирования, заменяется оператором погрешности ∆.

Посмотрим, как это делается при расчёте R:

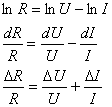                                                                                                                              (9)

Обратим внимание: знак "-" заменяется на"+", т.к. по логике вещей вклад в ошибку результата вносят измерения всех величин (т.е.ошибка накапливается, суммируется и не может компенсироваться за счёт каких-либо других погрешностей).

Рассмотрим в качестве примера расчёт плотности материала цилиндрического образца.

Данные для расчёта:

Диаметр D = 15.1±0.1мм

Высота Н = 45.1± 0,1мм

 Масса образца т = 18.4±0.1г

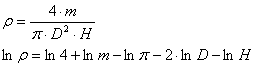(10)

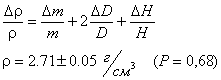                                                                                                      (11)

Согласно принятому правилу, конечная информация должна содержать столько значащих
цифр, сколько содержится в исходной, при этом ориентиром является результат с наименьшим
числом значащих цифр. В погрешности измерений принято оставлять одну лишь значащую
цифру; результат и погрешность заканчиваются  в одном десятичном разряде (обыкновенные дроби использовать не принято).

Что касается уровня надёжности результата (вероятность Р), то конечная вероятность
определяется уровнем начальной вероятности. В приведённом примере начальная вероятность
всех результатов равна 0,68.  Другие варианты мы не рассматриваем, с ними можно

познакомиться в специальной литературе.

Следует отметить, что приведённая здесь методика аттестации результатов в тех случаях, когда доминирующими являются погрешности случайного характера имеет предварительный и недостаточно строгий характер. Она даёт относительно надёжные результаты при достаточно большом объёме выборки экспериментальных данных.

Но на практике приходится иметь дело с микростатистиками, когда набор экспериментальных данных очень ограничен. Более надёжные суждения о доверительном интервале в таком случае можно получить, используя критерии   Стьюдента. В соответствии с