Методи ЕЦП в полі та групі точок ЕК і їх властивості

ЛЕКЦІЯ № 16(3.4)

 З ДИСЦИПЛІНИ 

«ОСНОВИ ТЕОРІЇ ЗАХИСТУ ІНФОРМАЦІЇ»

Тема лекції

« Методи ЕЦП в полі та групі точок ЕК і їх властивості»

Навчальні питання

16.1 МЕТОДИ ЕЦП В ПОЛІ Галуа»( Х9.30, FIPS–186 – 1, ГОСТ Р 34.10 - 94, ГОСТ 34.310–95).

16.2  ЕЦП в групі точок еліптичних кривих та його стійкість.

16.3  Метод ЕЦП, що реалізований в  національному стандарті (ДСТУ 4145-2002).

16.4 СУТНІСТЬ ЕЦП ГОСТ Р 34.10-2001

Джерела що рекомендуються для  самостійної робот

1.  Горбенко І.Д. Основи теорії захисту інформації. Електронний конспект лекцій. Харків, ХНУРЕ, 2005 р.

2.  Горбенко І.Д. „Криптографічний захист інформації”. Навч. посібник Харків, ХНУРЕ, 2004 р.

3. В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

 Додаткова література

1.  А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

2.Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

3. Закон України « Про електронний цифровий підпис»

16.1МЕТОДИ ЕЦП В ПОЛІ Галуа»( Х9.30, FIPS–186 – 1, ГОСТ Р 34.10 - 94, ГОСТ 34.310–95).

Алгоритми ЕЦП FIPS–186 - 1 (DSA) та  ГОСТ 34.310-95 дуже схожі та пройшли випробовування часом. Ці алгоритми продовжують застосовуються дуже широко.Так в Fips–186-3 передбачається продовжити використання DSA. По суті в них використовується криптографічний алгоритм перетворення Ель – Гамаля за двома модулями P та  q. Загальносистем­ними параметрами являються  для  DSA  або для ГОСТ 34.310-95, де Р є просте «сильне» число, q – також просте число, але яке входить в канонічний розклад  числа Р – 1, а g – первісний елемент простого поля. В таблиці 16.1  наведені вимоги відносно цих загальносистемних параметрів.

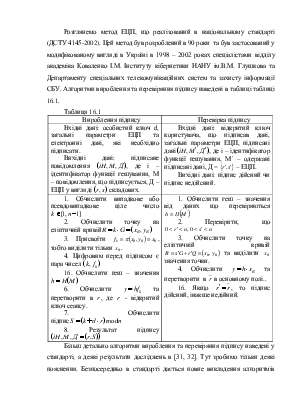
Таблиця 16.1

 Вказані загальносистемні параметри можуть бути для всіх користувачів одинакові і змінюватись дуже рідко. В Fips–186-3 обмеження на загальні параметри інші.

Виробка ЕЦП для ГОСТ 34.310-95

В таких ЕЦП застосовується схема Діфі-Хелмана розповсюдження ключів. Кожен користувач формує довгостроковий  особистий ключ , причому  ,

а потім обчислює відкритий ключ 

                                      (16.1)

Відкритий ключ сертифікується  та в подальшому його сертифікат повинен бути доступним усім користувачам, які отримують від нього підписані дані .

Обчислення ЕЦП здійснюється у такому порядку.

1.   Для М, обчислюється геш – значення  h = H(M), причому  в якості ХФ використовується ГОСТ 34.311-95. Якщо h = 0, то вона змінюється .

2.  Генерується випадково або псевдовипадково ключ сеансу k , причому .

3.   Обчислюється значення , тобто за модулем Р, потім за  другим модулем  відкритий ключ сеансу

                                                (16.2)

 Далі обчислюється безпосередньо підпис

                                                                                                                                                      (16.3)

Підписані дані мають такий вигляд     М; (r, S).

Перевірка ЕЦП повинна виконуватись у такому порядку.повідомлення

Користувачеві що перевіряє підпис відомо:

-  підписані дані ;

-  загальні параметри  та сертифікат відкритого ключа Y 

 Необхідно перевірити цілісність, справжність та встановити авторство даних М .

Перевірка ЕЦП виконується у такому порядку.

1.  Перевіряється умова що  ,

2.  Обчислюється геш – значення від даних, що перевіряються

3.  Обчислюються додаткові дані:

;

    ;

    .

4.  Обчислюєтьсязначення                                                                                       (16.4)

5.  Здійснюється перевірка виконання умови що . Якщо порівняння виконується то дані вважаються цілісними та  справжніми і визнається їх авторство. Інакше дані відкидаються.

В стандарті Fips–186 для очислення ЕЦП використовується наступна формула

      S=(h + x r)/k(modP)(mod q)                        (16.5)

Підписом в цьому стандарті є також пара цілих чисел  (r, S).

16.2  ЕЦП в групі точок еліптичних кривих.

Наприкінці ХХ століття було встановлено, що складність вирішення дискретного рівняння відносно особистого ключа,