Методи ЕЦП в полі та групі точок ЕК і їх властивості, страница 2

тобто складність знаходження   Xносить субекспонентний характер. Наприклад,  при розмірі модуля Р=2 складність з застосуванням загального решета числового поля буде складати всього порядку 10операцій множення з числами відповідного розміру. В той же час згідно сьогоднішніх досягнень

вирішення порівняння

                                      (16.6)

відносно носить експонентний характер і, наприклад,  при порядку базової точки n = 2 з застосуванням методу  - Полларда складає  приблизно 10 операцій  складання точок на еліптичній кривій. Таким чином, складність вирішення дискретного логарифмічного рівняння в групі точок еліптичної кривої незрівнянно вище. Це  в основному і визначило широке застосування та прийняття відповідних стандартів криптографічних перетворень на основі перетворень в групі точок еліптичних кривих.

 В той же час показано, що для (16.1) складність криптоаналізу  носить субекспонентний характер , тобто визначається як

,                                         (16.7)

де  – параметри метода криптоаналізу.

Для криптоперетворень в групі точок ЕК

, де .                          (16.8)

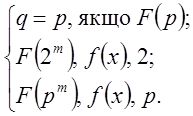
 – базова точка на еліптичній кривій, яка має наступні властивості:

-  над полем  координати базової точки : ;

-  над полем  – поліноми не вище  ступеню;

-  над полем  – поліноми не вище  ступеню.

Порядок поля :

                                           (16.9)

 – особистий ключ, .

 – відкритий ключ, точка на еліптичній кривій з координатами .

Задача криптоаналітика – знайти особистий ключ . Показано, що найбільш ефективний метод розв’язку (2.4.10) відносно  являється ρ-Поларда метод. Складність цього методу можна оцінити як:

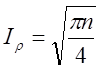,                                         (16.10)

де  – порядок базової точки.

В подальшому ми отримаємо більш точні оцінки складності криптоаналізу.

16.3  Метод ЕЦП, що реалізований в  національному стандарті (ДСТУ 4145-2002).

Розглянемо метод ЕЦП, що реалізований в національному стандарті (ДСТУ 4145-2002). Цей метод був розроблений в 90 роки  та був застосований у модифікованому вигляді в Україні в 1998 – 2002 роках спеціалістами відділу академіка Коваленко І.М. Інституту кібернетики НАНУ ім.В.М. Глушкова та Департаменту спеціальних телекомунікаційних систем та захисту інформації СБУ. Алгоритми вироблення та перевіряння підпису наведені в таблиці таблиці 16.1.

Таблиця 16.1

Вироблення підпису	Перевірка підпису
Вхідні дані: особистий ключ d, загальні параметри ЕЦП та електронні дані, які необхідно підписати. Вихідні дані: підписане повідомлення , де i – ідентифікатор функції гешування, М – повідомлення, що підписується, Д – ЕЦП у вигляді  складових.	Вхідні дані: відкритий ключ користувача, що підписав дані, загальні параметри ЕЦП, підписані дані, де i – ідентифікатор функції гешування, М΄ – одержані підписані дані, Д =  – ЕЦП. Вихідні дані: підпис дійсний чи підпис недійсний.
1. Обчислити випадкове або псевдовипадкове ціле число 2. Обчислити точку на еліптичній кривій 3. Присвоїти , тобто виділити тільки . 4. Цифровим перед підписом є пара чисел 16. Обчислити геш – значення 6. Обчислити  та перетворити в , де  - відкритий ключ сеансу. 7. Обчислити підпис 8. Результат підпису	1. Обчислити геш – значення від даних що перевіряються 2. Перевірити, що 3. Обчислити точку на еліптичній кривій  та виділити  значення точки. 4. Обчислити  та перетворити  в  в основному полі.. 16. Якщо , то підпис дійсний, інакше недійний.

Більш детально алгоритми вироблення та перевіряння підпису наведені у стандарті, а деякі результати досліджень в [31, 32]. Тут зробимо тільки деякі пояснення. Безпосередньо в стандарті дається повне викладення алгоритмів вироблення та перевірки підпису, причому криптографічне перетворення виконується в групі точок еліптичної кривої над полем F(2, де m –  степінь незвідного полінома. Особливістю ЕЦП ДСТУ 4145-2002 є те, що степінь незвідного полінома m може змінюватись в інтервалі від 163 і до 509 і відповідно буде змінюватись порядок базової точки n майже у тих же межах. Пункти 1 – 4 алгоритму вироблення підпису можуть бути виконаними попередньо і накопичений масив різних значень перед підписів  можна використовувати в процесі виконання підпису, але знищуючи уже використані перед підписи. Крім того, якщо масив підписів зберігається, то відносно них повинна бути забезпечена конфіденційність такого ж рівня, як і відносно особистого ключа. Використаний особистий ключ сеансу повинен бути знищеним після обчислення ЕЦП.