Полиномы Чебышева

Рассмотрим  часто  встречающийся  случай.   Представим  себе,  что  строя  график  мы

обнаруживаем, что линия имеет сходство с параболой . Нам остаётся наилучшим образом определить параметры зависимости а, b, с. Составим следующие математические формы:

Коэффициенты а, , с находятся решением системы уравнений:

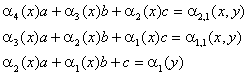
Если парабола второй степени не подходит, то теоретически аппроксимирующую    функцию

можно взять в виде многочлена любой степени. Однако, практически мы сталкиваемся с трудным случаем, т.к. определитель системы будет близок к нулю и решение станет не устойчивым.

В подобных случаях обычно поступают так: представляют сглаживающую функцию в виде:

,

где φ_l(х) - полиномы Чебышева.

Полиномы Чебышева интересны тем, что они обладают свойством ортогональности:

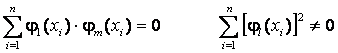
форма для коэффициентов c_lвыглядит достаточно просто:

.

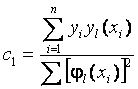Для расчетов самих полиномов Чебышева имеются специальные машинные подпрограммы или готовые таблицы. Можно попытаться представить экспериментальные результаты в виде двухпараметрических зависимостей y=(a,b,x).