Информатика и выч. техника \ Основы теории защиты информации

Вступ в криптоаналіз RSA криптосистем, страница 6

    292 º 51(mod 209)

    312 º 53(mod 209)

    (3129)2 º 5 4(mod 209); (2931)2 º 25 2(mod 209);

x=63; y=25; (x-y, 209) НСД=(38, 209)=(219, 209) = 19

Використовуючи алгоритм Евкліда маємо:

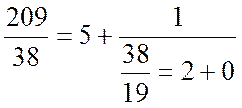
a1 = 209; a2 = 38

P=209:19=11;Q=19

209:38=5; r=19

a1 = 38; a2 = 19

39:19=2; r=0;

НСД (a1, a2)=a2 = 19

Тепер розв’яжемо ключове порівняння

Dk = 103; N=209; j(N)= 10*18 = 180

j(N) (-k)+DkEk = 1;         180(-k)+103Ek = 1

180x+103y = 1       x=(-1)m+1bm-1;          y = (-1)mam-1;

.

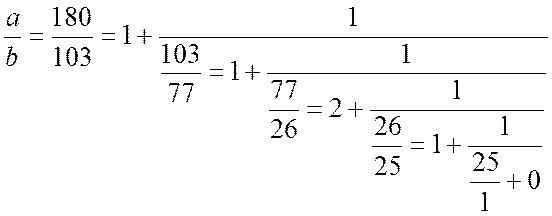r0 = 1;

r1 = 1;

r2 = 2;

r3 = 1;

r4 = 25;

m = 4;

am-1 = rm-1am-2+am-3;  bm-1 = rm-1bm-2+bm-3;

a3 = r3a2 + a1;                   b3 = r3b2 + b1;

;

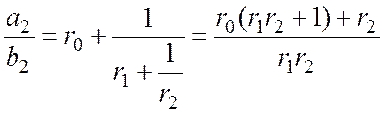a2 = 1(1*2+1)+2 = 5; b2 = 3;

a3 = 7;

y = (-1)47 = 7.

Таким чином Ek = 7.

В таблиці 1.14 наведені значення складності криптоаналізу, I1 – методом Ленстри, І2 – з використанням квадратичного решета.

.

.

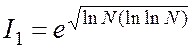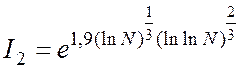Таблиця 1.14 – Значення складності криптоаналізу

N

lnN

lnlnN

(lnN)1/3

(lnlnN)2/3

I1

I2

256

179,2

5,29

5,64

2,99

1,7×1013

8,2×1013

512

358,4

5,98

7,10

3,25

8,5×1019

1,2×1019

768

537,6

6,29

8,13

3,41

1,7×1024

7,4×1022

1024

716,8

6,57

8,94

3,51

6,3×1029

7,8×1025

2048

1433,6

7,26

11,27

3,74

2,4×1044

6×1034

4096

2867,2

7,96

14,20

3,99

4,1×1065

5,6×1046

8192

5734,4

8,65

17,89

4,21

5,3×1096

1,4×1062

Перевірка Ek*Dk = 103*7 = 721(mod 180)º1 (mod 180). Тоді розв’язок зроблено правильно.

1.14.2 Задачi для самостiйного розв'язання

1. Факторизуйте модуль  RSA перетворення методом двійкового решета, якщо

№

1

2

3

4

5

6

7

8

9

10

11

N

391

221

299

209

247

133

217

253

161

91

437

2. Порівняйте складність криптоаналізу RSA, якщо використовуються метод –Полларда, метод Ленстри, квадратичне решето та загальне решето числового поля.

Визначте складність криптоаналізу, якщо довжини модулів  бітів.

1.14.3 Контрольнi запитання та завдання

1.  Сутність методу квадратичного решета?

2.  Як розраховується база квадратичного решета?

3.  Як рекомендується обирати значення числа Z?

4.  Викладіть сутність двійкового решета?

5.  В чому сутність алгоритму Евкліда та які умови його застосування?

6.  Скільки розкладів таблиці квадратичного решета мають бути позитивними?

7.  Як оцінити стійкість RSA криптоперетворень?

8.  Яким чином стійкість криптоперетворень залежить від методу криптоаналізу?

9.  В чому суть методики RSA криптоаналізу?

10.  Дайте оцінку складності криптоаналізу різних етапів його виконання.

11.  Які вимоги ставляться до простих чисел, щоб складність крипто-аналізу була найбільшою?

12.  Як RSA перетворення може бути використане для здійснення цифрового підпису?

13.  Як RSA перетворення може бути використане для здійснення направленого шифрування?

14.  Які вимоги висуваються до пари ключів RSA-перетворення?

15.  Які канали вразливості властиві RSA-перетворенням?

16.  Порівняйте складність основних мотодів факторизації складених
чисел.

Скачать файл