Вступ в криптоаналіз RSA криптосистем, страница 2

Число десяткових знаків	Приблизне число бітів	Дата вирішення	Необхідне число MIPS-літ	Використаний алгоритм
100	332	Квітень 1991 р.	7	Квадратичне решето
110	365	Квітень 1992 р.	75	Квадратичне решето
120	398	Червень 1993 р.	830	Квадратичне решето
129	428	Квітень 1994 р.	5000	Квадратичне решето
130	431	Квітень 1996 р.	500	Загальне решето числового поля
140	464	Лютий 1999 р.		Загальне решето числового поля
150	498	Відкритий	Відкликаний
155	514	Серпень 1999 р.		Загальне решето числового поля
160	531	Квітень 2003 р.		Загальне решето числового поля
174	576	Грудень 2003 р.		Загальне решето числового поля
193	640	Відкритий
212	704	Відкритий
232	768	Відкритий
270	896	Відкритий
309	1024	Відкритий
463	1536	Відкритий
617	2048	Відкритий

До 1994 року для розкладання на множники застосовувався підхід, відомий за назвою методу квадратичного решета. Для криптоаналізу RSA-130, RSA-140, RSA-155, RSA-160, RSA-576 використовувався новий алгоритм, названий методом решета в полі чисел загального виду, що дозволило скоротити обсяг обчислювальних зусиль майже на 10% у порівнянні з тими, що були потрібні раніше для аналізу RSA-129.

Погроза ключам великої довжини тут подвійна: безупинне зростання обчислювальної потужності сучасних комп'ютерів і безупинне удосконалення алгоритмів розкладання на множники.

3.2.3 Двійкове решето

Базується на знаходженні двох випадкових чисел Х і Y, але таких, що:

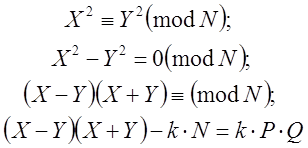
1) ;

2) ;

3) ;

4).

У випадках 3, 4 просте число може буде знайдено, як:

НСД;

НСД.

Сутність методу двійкового решета:

1. Будується база двійкового решета:

 (добуток простих чисел)

2. .

Приклад

Нехай необхідно факторизувати число .

Будуємо базу:

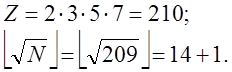
Розрахунок зводиться в табл. 3.2.1

Таблиця 3.2.1

і			Р1	Р2	...	Р3
1	225	16	4			+
2	256	47	-			-
3	17	80	4		1	+
4
l

і – номери дослідів

Необхідно одержати позитивних результатів не менше числа в базі

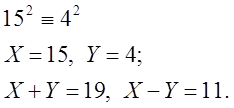
НСД = НСД=11

11·19 = 209.

3.2.4 Сутність методу ρ-Поларда

Метод ρ-Поларда є попередником методу двійкового решета. Його розв’язок полягає у знаходженні Х і Y, які порівнюються за  

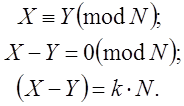
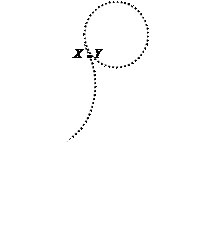Сутність методу: за допомогою деякої функції  будується послідовність точок (крива ρ-Поларда):

Точка Х повинна збігтися з точкою Y.

НСД.

Додаток А

1.13 Криптоаналіз RSA та дискретних логарифмiв методом -Поларда. Приклади розв’язку задач та задачі для самостійного розв’язання

1.13.1 Приклади розв'язку задач