Изучение свойств излучения оптического квантового генератора на смеси гелия и неона (лабораторная работа), страница 8

8.  Рассчитать среднеквадратичную ошибку в определении длины волны  по формуле:

.

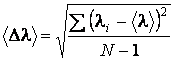9.  Произвести интервальную оценку величины , используя  – распределение Стьюдента для доверительной вероятности 0,95. В качестве истинной величины математического ожидания выбрать табличное значение _табл.=6,328×10^{-7 м. Интервальная оценка определяется по формуле:}

,

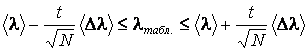где – случайная величина Стьюдента, зависящая от объема выборки  (числа экспериментальных точек). Значения  для доверительной вероятности 0,95 приведены в таблице 4.1.

Таблица 4.1

При возрастании  ® 2.

10.  Записать в отчет, в каких пределах лежит доверительный интервал для  и попадает ли в него значение _табл..

11.  Записать в отчет символически состояние с инверсной населенностью атома неона и соответствующие метастабильные состояния в атоме гелия,  совпадающие по энергиям с этими состояниями (рисунок 1.4).

12.  Записать символически переход, который обеспечивает генерацию излучения с длиной волны , полученной в эксперименте. Воспользоваться для этого схемой энергетических уровней неона (рисунок 1.4).

13.  Найти по совокупности измеренных значений диаметр пятна в метрах его среднее значение .

14.  Определить угол расходимости лазерного луча  в радианах по формуле:

,

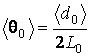где  м – расстояние, которое луч лазера проходит от выходного зеркала до экрана.

15.  Рассчитать диаметр пятна  и его площадь  на расстояниях от выходного зеркала лазера 1, 5, 10, 50, 100, 3,8×10⁸ м, используя для этого величину угла расходимости , полученные в эксперименте по формулам: