Энергия затухающих колебаний. Вынужденные колебания. Волны. Электромагнитные волны (Главы 8-10 учебного пособия по общей физике)

7.5.  Энергия затухающих колебаний

Энергию осциллятора с потерями энергии можно рассчитать с помощью тех же формул, которые получены для идеального осциллятора.

Особенностью реального осциллятора является то, что амплитуда его колебаний с течением времени уменьшается.

Поскольку полная энергия осциллятора прямо пропор-циональна квадрату амплитуды, постольку и полная энергия реального осциллятора будет уменьшаться с течением времени.

Выражения для расчёта энергии реального осциллятора имеют следующий вид:

для пружинного маятника

;

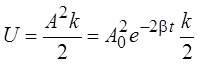энергия математического маятника с потерями энергии

.

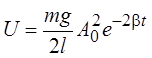Энергия, запасённая в колебательном контуре, сопротивление которого отлично от нуля, может быть найдена следующим образом:

.

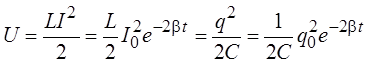Таким образом, полная энергия осциллятора с потерями энергии уменьшается с течением времени по экспоненциальному закону.

Обратите внимание: скорость уменьшения энергии осцил-лятора в два раза выше скорости уменьшения амплитуды колебаний осциллятора.

8. Вынужденные колебания

Любой осциллятор (например, пружинный маятник) может испытывать внешнее воздействие. Если внешнее воздействие периодическое, то возникнут вынужденные колебания осцил-лятора. Характер колебаний осциллятора определяется как внеш-ним воздействием, так и свойствами осциллятора.

8.1  Вынужденные колебания пружинного маятника

Рассмотрим поведение пружинного маятника, на который кроме силы трения действует внешняя сила, изменяющаяся по гармоническому закону: F = F_о×coswt.

Уравнение движения для него в этом случае будет иметь вид

,

.

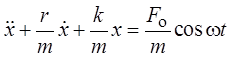Введём коэффициенты 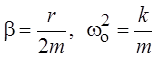. Теперь дифферен-циальное уравнение принимает вид

.

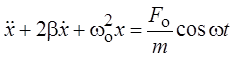Получили неоднородное дифференциальное уравнение второ-го порядка. Общее решение такого уравнения является суммой общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения уже было получено. Оно описывает затухающие колебания , где . Эти колебания возникают сразу после первого толчка внешней силы и по истечении некоторого времени затухают.

Для того чтобы найти частное решение неоднородного урав-нения, отметим следующее.

В правой части уравнения стоит функция 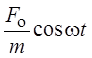, которая описывает гармоническое колебание с начальной фазой, равной нулю.

Следовательно, сумма слагаемых в левой части диффе-ренциального уравнения должна представлять собой такое же гармоническое колебание.

Как показано в разд. 6.3.1 результатом сложения нескольких одинаково направленных гармонических колебаний с одина-ковыми частотами является гармоническое колебание. Поэтому каждый из членов суммы  представляет собой гармоническое колебание, частота которого равна частоте внешнего воздействия w.

Допустим, что колебания х отстают по фазе от колебаний внешней силы на j: x = Acos(wt-j). Тогда слагаемое  можно записать следующим образом: .

Взяв производную от х по времени и умножив её на 2b, получаем  .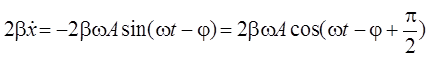

Вторая производная от ко-ординаты маятника по времени равна .

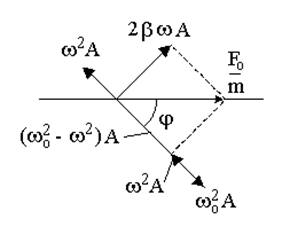
Амплитуда А и начальная фаза j колебаний х являются неизвестными величинами. Для того чтобы найти выражения для расчёта этих величин, восполь-зуемся векторной формой пред-ставления гармонических коле-баний.

В момент времени t = 0 фаза силы внешнего воздействия равна нулю, поэтому колебание 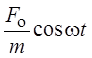 будет представлено горизонтальным вектором .

Как уже отмечаось, . Это колебание будет представлено вектором , который расположен под углом -j относительно вектора .

Второй член суммы 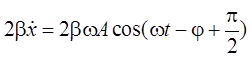 опережает по фазе  на p/2. Следовательно, вектор 2bwА распо-ложен под углом 90^о относительно вектора .

Первый член суммы  имеет фазу, равную фазе третьего, но противоположен ему по знаку, поэтому представлен вектором , который направлен против вектора .

Сумма этих векторов равна вектору , что и показано на векторной диаграмме.

Из векторной диаграммы на основе теоремы Пифагора получаем, что

.

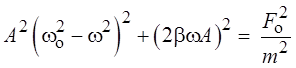Выражая отсюда А, получаем

.

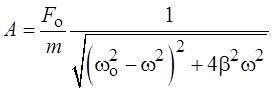Из векторной диаграммы также видно, что тангенс угла j равен

.

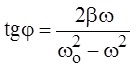Таким образом, частное решение дифференциального уравне-ния имеет следующий вид:

.

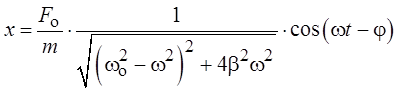Это выражение описывает установившиеся вынужденные колебания системы.

Наличие в решении гармонической функции cos(wt-j), го-ворит о том, что под воздействием внешней гармонической силы осциллятор будет совершать гармоническое колебание с цикли-ческой частотой w, равной циклической частоте внешней вынуж-дающей силы.

Амплитуда А и разность фаз j этих колебаний зависят от параметров осциллятора (w_о, b) и от частоты внешнего воз-действия w.

Как уже отмечалось, об-щее решение рассматривае-мого дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного 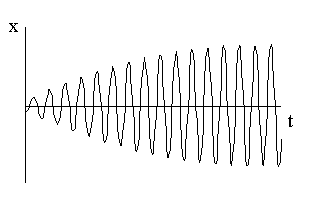уравнения, поэтому сразу после начала внешнего воз-действия колебания осцил-лятора будут представлять собой результат сложения двух колебаний – затухаю-щего с частотой w¢ и гар-монического с частотой внешнего воздействия w. По-степенно амплитуда зату-хающих колебаний становится пренебрежимо малой, а колебание – гармоническим (см. рисунок).

8.2.  Вынужденные колебания в колебательном

контуре