Функции многих переменных. Дифференцируемость и дифференциал функции в точке, страница 2

Т2. Если функции f:X->R и g:X_.R определены на X  и дифференцируемы в точке х Î Х, то для них:

1)(2), 2)(3)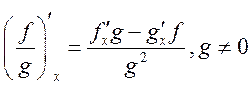. Отношения 2 и 3 для дифференциалов имеют вид: d(fg)=gdf+fdg; d(f/g)=(gdf-fdg)/g². Аналогичные соотношения верны и для частных производных.

Т3. Если f:X->Y, X пордпростр-во R^m, Y – подпростр-во Rⁿ дифференцируема в точке х Î Х, а отображение g:Y->R^k  дифференцируемо в точке y=f(x). Тогда композиция отображений  тоже дифференцируема в точке ч и дифференциал композиции = композиции дифференциалов. . Причем - произведение матриц Якоби.

Производная по вектору и градиент функции в точке. Если функция f(x) определена в некоторой окрестности x₀, а v – некоторый вектор Î R^m . 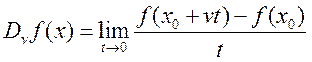. Эта величина называется производной функции f  в точке x₀ по вектору v (по направлению v). В частности, если рассмотреть базисные векторы e_i , то производная по вектору v в точке x₀:  (9)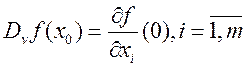.  Если пространство R^m рассматривать, как Евклидово Пространство, то " лин. функцию L(v) можно записать в виде скалярного произведения (ξ, v), ξ – некоторый вектор пространства R^m , определяемый линейной функцией L(v). А раз это верно в общем случае, то (11) .

Градиент: Вектор ξ из 11 называется градие0нтом функции f в точке x₀ и обозначается ξ=gradf(x₀). А значит 11-> (12) ->(grad(f(x₀)),v). Если в пространстве R^m выбрана декартова система координат, то 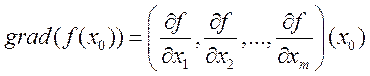(13). Производную по единичному вектору данного направления называют производной в заданном направлении

Теорема о среднем: Пусть f:G->R вещественнозначная функция, определенная в области G из R^m . Пусть отрезок [x;x+h] из G. Если при этих условиях функция непрерывна в точках [x;x+h] и дифференцируема в т. (x;x+h), то имеет место равенство: f(x+h)-f(x)=f’(ξ)h (1).

Достаточное условие дифференцируемости: Пусть f:U(x)->R. Если функция f имеет в " точках U(x) все частные производные, то  из непрерывности этих частных производных следует дифференцируемость функции в этой точке.

Частные производные высшего порядка:

Функция 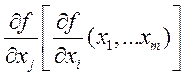 называется 2ой производной функции по переменной x_i,x_j b обозначается 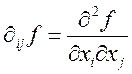. Аналогично определяются к-ые, к+1-ые производные.

Теорема. Если f:G->R имеет в области G вторые частные производные, то в каждой точке области G, в которой обе этих производных непрерывны их значения совпадают. . Т.е. если f – к-раз дифференцируемая функция, то значения к-ой частной поризводной не зависят от порядка дифференцирования.

Формула Тейлора: Если f: U(x)->R определена и принадлежит классу Сⁿ(U(x)), то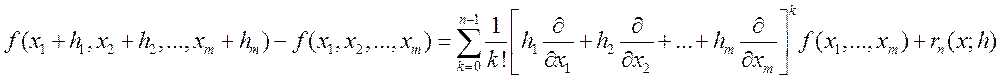

Где 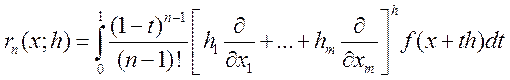 - остаточный член в интегральной форме. То что стоит в квадратных скобках называется формальным оператором дифференцирования.

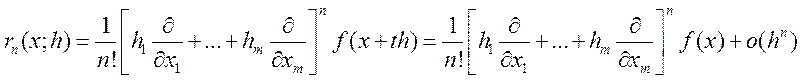 - Остаточный член в форме Лагранжа.

Экстремумы функций многих переменных: Говорят, что f:G->R имеет локальный максимум(минимум) во внутренней точке x₀ множества G, если $ такая U(x₀) для которой для всех точек этой окрестности f(x)≤f(x₀) (f(x)≥f(x₀)). Если неравенство строгое, то в точке x₀ $ строгий локальный максимум(минимум).

Теорема о необходимом условии существования экстремума: Пусть f определена в точке x₀ и имеет в ней частные производные первого порядка по веем переменным. Тогда для того, чтобы функция имела в точке x₀ локальный экстремум необходимо, чтобы в ней(1)

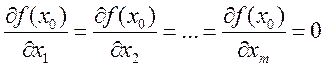
Точка x₀ называется критической точкой f:U(x₀)->Rⁿ , если ранг матрицы Якоби отображения f в этой точке < наименьшего из n,m: rg(J(f(x₀)))<min(m,n)

Теорема о достаточном условии существования экстремума: Пусть f:U(x₀)->Rⁿ, где f Î C². Она определена в U(x₀) и пусть x₀ – критическая точка функции f. Тогда, если в разложении(2)  функции f квадратичная форма (сумма) а)знакоопределена, то в точке x₀ f имеет локальный экстремум(минимум если положительно определена, максимум, если отрицательно) б)иначе не имеет экстремума в этой точке

График функции z=f(x;y), где f:G->R это есть некоторое множество S={(x,y,z) Î R³ | (x,y) Î G, z=f(x;y)}

Координаты т. (x;y) на поверхности S называются криволинейными координатами на поверхности S.

Касательная плоскость к графику функции. Если z=f(x;y)дифференцируема в точке (x₀,y₀), это значит, что (1).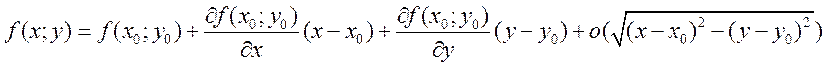

Уравнение плоскости в R³ (2)z=z₀+A(x-x₀)+B(y-y₀). Сравнив формулы 1 и 2: функция в U(x₀) может быть однозначно представима в виде(3) [1 без о(корня)]. Плоскость 2 называется касательной плоскостью к f(x;y) в точке (x₀,y₀,f(x₀;y₀))

Нормальный вектор. Из уравнения плоскости 3: вектор с координатами(5): 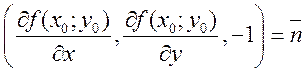 будет нормальным вектором касательной плоскости. Направления этого вектора считается нормальным или ортогональным к поверхности S в точке с координатами (x₀,y₀,f(x₀;y₀)).

Теорема о неявной функции.