



Министерство Общего и Профессионального образования
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Лабораторная работа №3 по курсу
“Программирование вычислений”
Факультет: ПМИ
Группа: ПМ-31
Студенты: Артемьев М.
Гребенюк А.
Тутов А.
Преподаватели: Рояк С. Е.
Токарева М. Г.
Новосибирск
2005
1. Вариант задания:
13.2. Умножение 7-диагональной несимметричной матрицы на вектор
2. Математическая модель:
|
Дано:
Результат:
|
Решение: Пусто есть матрица
В силу симметрии профиля два последних действия могут быть объединены в одном цикле. |
1. Алгоритм:
Матрица ![]() представлена
следующим образом:
представлена
следующим образом:
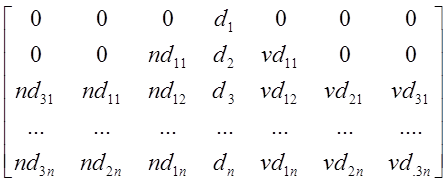 ,
,
где: ![]() - i-ый элемент главной диагонали матрицы А;
- i-ый элемент главной диагонали матрицы А;
![]() - j-ый
элемент i-ой верхней диагонали;
- j-ый
элемент i-ой верхней диагонали;
![]() - j-ый
элемент i-ой нижней диагонали;
- j-ый
элемент i-ой нижней диагонали;
Количество нулей в столбце определяется следующим образом:
1 для 3-ого и 5-ого столбца;
![]() для 2-ого и 6-ого;
для 2-ого и 6-ого;
![]() для 1-ого и 7-ого.
для 1-ого и 7-ого.
1) Умножение
диагонали матрицы ![]() на вектор В.
на вектор В.
for i=1, n, i=i+1
do
rez(i)=![]() (i,4)*B(i)
(i,4)*B(i)
end do
2) Умножение
верхнего и нижнего треугольника матрицы ![]() на
вектор В.
на
вектор В.
Введем дополнительный массив размером index(n) для хранения количества ненулевых элементов в строке (столбце). Фактически index(i) – что количество элементов, на которые нужно умножить строку(столбец).
А также массив temp(3), для хранения смещений элементов строки(столбца), построенный следующим образом:
temp(1)=2
temp(2)=n![]() +4
+4
temp(3)=![]()
Тогда
умножения верхнего и нижнего треугольника матрицы ![]() на
вектор В можно представить так:
на
вектор В можно представить так:
do i=2,n
do j=1, index(i)
k=i+j-temp(j)
rez(i) = rez(i) + ![]() (i,4-j)*B(k)
(i,4-j)*B(k)
//_в силу симметричности профиля
rez(k) =
rez(k) + ![]() (i,4+j)*B(i)
(i,4+j)*B(i)
enddo
enddo
4. Листинг:
program laba3
dimension Rmx(256*1024*256)
open(1, file='in1.dat')
read(1,*) n, n1,n2
*_проверка на корректность
if(n1+n2+3>n) goto 99
*_ввод матрицы
call enter(Rmx(1),Rmx(1+n*7),n,n1,n2)
*_умножение матрицы
call umnozh(Rmx(1),Rmx(1+n*7),Rmx(1+n*8),n,n1,n2)
*_вывод матрицы
call out(Rmx(1+n*8),n)
goto 1
99 print *,"Oshibka! Matrica ne 7-diagonal'naja!"
1 end
subroutine enter(Rmatrix,x,n,n1,n2)
dimension Rmatrix(n,7), x(*)
read(1,*)((Rmatrix(i,j),j=1,7),i=1,n)
read(1,*)(x(i),i=1,n)
end
subroutine out(Rmatrix,n)
dimension Rmatrix(*)
do i=1,n
write(*,1) Rmatrix(i)
end do
1 format (1x,G10.5)
end
subroutine umnozh(Rmatrix,x,rez,n,n1,n2)
dimension itemp(3),iindex(n)
dimension Rmatrix(n,7),x(*),rez(*)
*_промежуточный массив для хранения числа повторения цикла по j
iindex(2:n1+2)=1
iindex(n1+3:n1+n2+3)=2
iindex(n1+n2+4:n)=3
*_смещение элемента в строке (столбце)
itemp(1)=2
itemp(2)=n1+4
itemp(3)=n1+n2+6
*_главная диагональ
do i=1,n
rez(i)=Rmatrix(i,4)*x(i)
end do
do i=2,n
do j=1,iindex(i)
k=i+j-itemp(j)
rez(i)=rez(i)+Rmatrix(i,4-j)*x(k) !_нижный треугольник
rez(k)=rez(k)+Rmatrix(i,4+j)*x(i) !_верхний треугольник
enddo
enddo
end
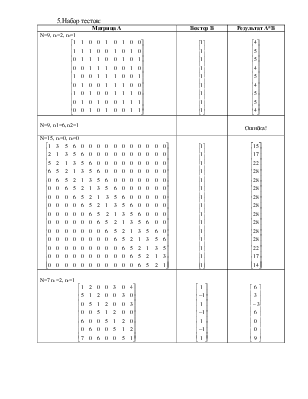
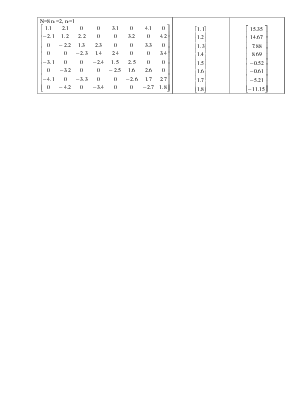
5.Набор тестов:
|
Матрица А |
Вектор В |
Результат А*В |
|
N=9, n1=2, n2=1
|
|
|
|
N=9, n1=6, n2=1 |
Ошибка! |
|
|
N=15, n1=0, n2=0
|
|
|
|
N=7 n1=2, n2=1
|
|
|
|
N=8 n1=2, n2=1
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.