

На основе метода переменных состояний возможен подход, при котором определяют дифференциальные уравнения, моделирующие этот фильтр. Этот метод позволяет решить более общую задачу – выделения с наименьшей погрешностью g2(t)=[b^(t)-b(t)]2 сообщения b(t) из наблюдаемого на конечном интервале времени сигнала z(t)=s(t, b)+n(t). Условие стационарности сигнала и помехи в рамках этого метода не обязательны. Относительно фильтруемого сообщения b(t) дополнительно предполагают, что оно порождается линейным стохастическим дифференциальным уравнением. В частом случае используют уравнение
(1)![]()
где n1(t) - нормальный белый шум с нулевым средним значением n1(t)=0 и односторонней спектральной плотностью N1. Сформированное т.о. сообщение b(t) является гаусовским марковским процессом с функций корреляции
B0(τ)=P0e-α|τ|, P0=N1/(4α), α=1/(RC).
Спектральная плотность мощности такого сообщения
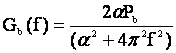
В более общем случае сообщение описывается системой линейных дифференциальных уравнении.
Рассмотрим случай линейной фильтраций, когда наблюдаемый процесс на входе фильтра задан уравнением
(2) z(t)=b(t) f(t)+n(t), 0≤t≤T,
а сообщение b(t) -уравнением (1). Здесь f(t) – известная функция (несущее колебание): b(t)f(t)=s(t,b) – передаваемый сигнал; n(t) – белый гаусовский шум с нулевым средним значением n(t)=0 и односторонней спектральной плотностью N0. Уравнение (2) является уравнением наблюдения, а (1) – уравнением состояния. На основе уловия оптимальной линейной фильтраций выводится соотношении, которое позволяет получить уравнения: (3)
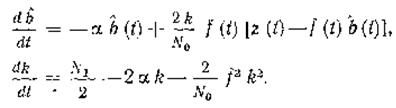 (4)
(4)
Уравнения
(3) и (4) принято называть уравнениями фильтра Калмана. Уравнение (3)
определяет алгоритм формирования оценки, структурную схему фильтра, а (4) –
ошибку фильтрации k=g2(t). Структурная
схема, моделирующая уравнение (3)- рис 1а. Построение схемы удобно начинать с
интегратора. Для этого обозначим правую часть через y(t)=y1(t) +y2(t), где
y1(t)=![]() f(t)[z(t)-f(t)b^(t)],
y2(t)= -αb^(t). Тогда
уравнение (3) запишется как db^/dt=y(t). Отсюда следует, что если на вход интегратора подать
напряжение y(t), то на его выходе получим оценку сообщения b^(t). Для
того чтобы сформировать напряжение y1(t), необходимо иметь генератор Г несущего колебания f(t), два
перемножителя, сумматор и усилитель с коэффициентом усиления 2k/N0. С помощью этих устройств осуществляются все
операции, входящие в выражение для y1(t). Напряжение y2(t) получается с помощью усилителя с коэффициентом
усиления α на вход которого поступает напряжение оценки b^(t). Суммарное
напряжение y(t)=y1(y)+y2(t) с выхода сумматора поступает на вход интегратора,
выход которого представляет оценку b^(t). Для
немодулированного сигнала, когда s(t,b) в (3) и (4) нужно положить f(t)=1 и
схема фильтра Калмана примет более простой вид (рис 1б).
f(t)[z(t)-f(t)b^(t)],
y2(t)= -αb^(t). Тогда
уравнение (3) запишется как db^/dt=y(t). Отсюда следует, что если на вход интегратора подать
напряжение y(t), то на его выходе получим оценку сообщения b^(t). Для
того чтобы сформировать напряжение y1(t), необходимо иметь генератор Г несущего колебания f(t), два
перемножителя, сумматор и усилитель с коэффициентом усиления 2k/N0. С помощью этих устройств осуществляются все
операции, входящие в выражение для y1(t). Напряжение y2(t) получается с помощью усилителя с коэффициентом
усиления α на вход которого поступает напряжение оценки b^(t). Суммарное
напряжение y(t)=y1(y)+y2(t) с выхода сумматора поступает на вход интегратора,
выход которого представляет оценку b^(t). Для
немодулированного сигнала, когда s(t,b) в (3) и (4) нужно положить f(t)=1 и
схема фильтра Калмана примет более простой вид (рис 1б).
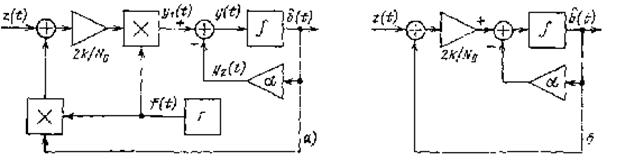
В качестве примера рассмотрим фильтрацию гаусовского марковского сообщения в канале с амплитудой модуляций, когда для передачи сообщения b(t) используется сигнал
(5) s(t, b)=b(t) sinω0t
Этот сигнал АМ с подавленной несущей. Уравнение наблюдения в этом случае
z(t)=b(t) sinω0t+n(t).
Уравнение оценки согласно (3)
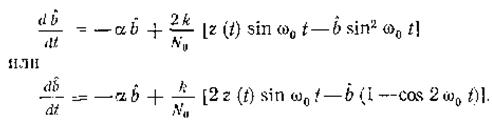
Можно пренебречь cos 2ω0t. Тогда имеем
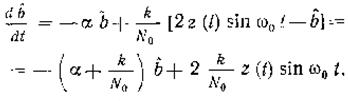
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.