3. Перечислите цепочки, выводимые из х (см. упражнение 2).
4. Выводима ли из х (см. упражнение 2) цепочка aaabbbbb?
5. Языком, порождаемым формальной грамматикой,
называется множество ___________, выводимых из ___________.
6. Определите язык, порождаемый грамматикой (см. упражнение 2).
7. Принадлежит ли цепочка 01011010 языку L(G), если G=<{0,1},{S, A, B},S,P>, где P={S®0S1½AS½BS1½e, A®S01½0A½1, B®1S0½B0½0}?
8. Определить язык, порожденный грамматикой G=<T,N,S,P>:
a) N={S, 0, 1}, T={a, b}, P={S®10a½1S, 0®b1, 1®a};
b) N={S, 0, 1, 2}, T={3, 4}, P={S®S312½302, 0®21,
12®4, 2®e};
c) N={S, A, B, C, D}, T={0, 1}, P={S®10A1½01B0½1CD1½D01,
A®0A1½1B1½0C, B®1C½0A11½B0, C®A10½B1,
D®10½A00½B0½1C};
d) N={S, 0, 1, 2, 3}, T={a, b, c}, P={S®013½S013, a2a®abca,
3®ab, 1a®caa, 0ca®c};
e) N={S, A, B, C, D}, T={0, 1}, P={S®0A0½1B0½1D1½0C1,
A®01B½B1, C1®A10½0A0, 1B®0C½C11,
D®A0½1C1½0D0½11½B00}.
9. Определите состав терминального и нетерминального словарей грамматики G=<T,N,S,P> с правилами
P={S®BC½AD½DE½SE½AB, A®EBD½AC½E, D®AB½DE½A,
ED®CB½AE½BC, C®A½BC½E, B®A½BCD, CB®A½B,
AEC®EC½AC½A}, если язык, порождаемый данной грамматикой, не пуст.
10. Построить грамматику, порождающую язык:
а) L={0n1k2n½n³1, k³0;
b) L={0n1m2m3n½n³1, m³1};
c) L={0n1n1m0m½n³1, m³1};
d) L={an111bm½n³1, m³n};
e) L={1n0am!!!bm02k½n³1, m³1, k³n};
f) L={(an=bn)(cm=dm)½n³1, m³1};
g) L={an–bm½n³1, m³1}U{ck+dk½k³1}.
Занятие 4. Операции над языками
Цель занятия: выработать навыки оперирования с формальными языками как с множествами заданной структуры. Уметь строить языки, используя основные операции над ними и уметь по заданной формуле языка определить, из каких простейших языков его можно построить и с помощью каких операций.
Что необходимо знать:
· основные понятия теории множеств (операции над множествами, эквивалентность множеств, отношения и их свойства) из курса дискретной математики,
· операции конкатенации и подстановки языка в язык,
· доказательство коммутативности диаграммы для операции объединения.
| | |
| | |
| | |
v v v
![]() L(G1) L(G2 ) ¾¾¾¾¾> L(G3)
L(G1) L(G2 ) ¾¾¾¾¾> L(G3)
Основные определения
1. Основные операции:
L3 = L1 È L2 = {x| x Î L1 или x Î L2};
L3 = L1 Ç L2 = {x| x Î L1 и x Î L2};
L3 = L1 \ L2 = {x| x Î L1 и x Ï L2};
L3 = L1 ° L2 = {x=yz| y Î L1,а z Î L2};
L3
= L* = 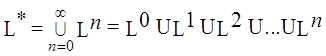 ,
,
где
![]()
при n > 1;
L3
= 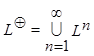
L3 = подстановка
языков L1, ....,Ln в язык L вместо символов
a1, ...,an есть операция, сопоставляющая языку L в
словаре T =
= {a1, ...,an} и языкам L1, ...,Ln
в словарях T1, ...,Tn соответственно следующий язык в
словаре T1 ![]() ...
...![]() Tn:
Tn:
{![]() Î
L,
Î
L, ![]() }
}![]() L^
L^
где L^ = {e},если eÎL и L^ = Æ, если е Ï L;
L3 = w\L = { j | wj Î L };
L3 = L/w = { j | jw Î L }.
2. Базовыми языками будем называть языки, которые не могут быть получены из других языков с помощью операций над этими языками. Например, L1 = {a}; L2 = {anbn |n ³ 1};
L3 ={anbncn | n ³ 1}.
Задачи и упражнения
a) L(G) = L1\(L2UL3), L1 = {w½wÎ{0,1}*},
L2 = {0w1½wÎ{0,1}*}, L3 = {0w0½wÎ{0,1}*}.
b) L(G) = L2\L1, L1 = {b2w½wÎ{a,b}*}, L2 = {w–1½wÎ{a,b}*}.
c) L(G) = L1UL2, L1 = {0n1n½n³2}, L2={w½wÎ{0,1}*}.
d) L(G) = L1\L2, L1 = {w½wÎ{0,1}*}, L2 = {0n1n½n ³ 1}
e) L(G) = L1IL2, L1 = {01n1n0½n ³ 1}, L2 = {01m0½m ³ 0}.
f) L(G) = L2\L1, L1 = {ab2ka½k ³ 0}, L2 = {abma½m ³ 1}.
a) N = {S, A}, T = {a, b}, P={S® aAb, A® aAb½e};
b) L(G) = {anbncmdm½n ³ 1, m ³ 1},
c) L(G) = L1UL2, L1 = {anbn½n³1}, L2 = {0m1m2m½m ³ 1}.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.