Задание 2. Построить инварианту
k:=0; d:=x; n:=y;
if d≠0 then
do
if d mod 2≠0 then k:=k+n fi
d:= d div 2; n:= 2*n; until d=0;
Два полезных свойства:
1) d mod 2 = d – 2(d div 2)
2) Т.к. [(A div B) div C] = A div (B*C), то
![]()
![]()
![]()
![]()
![]() (…(((d div 2) div 2) div
2) …div 2) = d div 2m (1)
(…(((d div 2) div 2) div
2) …div 2) = d div 2m (1)
m раз
Поскольку данный цикл продолжается до тех пор, пока d не станет равен 0, а начальное значение d является x, то цикл закончится, когда x div 2m = 0.
Следовательно, x div 2m-1≠ 0.
Отсюда, x = 2m-1 * 2ε, где 0≤ε<1
Найдем m: log2x = (m-1) log22 + ε
m-1 = log2x – ε
m = log2x + 1 – ε
m = (log2x + 1) div 1, т.е. целая часть log2x + 1
Если включить в рассмотрение x<0, то необходимо использовать |x| и тогда:
m = (log2|x| + 1) div 1, x≠0 (2)
Рассмотрим данный цикл, определив k0 = 0, d0 = x, n0 = y, x≠0, x – целое
|
x |
1 |
2 |
3 |
4 |
5 |
||||||||||
|
Шаг |
k |
d |
n |
k |
d |
n |
k |
d |
n |
k |
d |
n |
k |
d |
n |
|
0 |
0 |
x |
y |
0 |
x |
y |
0 |
x |
y |
0 |
x |
y |
0 |
x |
y |
|
1 |
y |
0 |
2y |
0 |
1 |
2y |
y |
1 |
2y |
0 |
2 |
2y |
y |
2 |
2y |
|
2 |
2y |
0 |
22y |
3y |
0 |
22y |
0 |
1 |
4y |
y |
1 |
4y |
|||
|
3 |
4y |
0 |
23y |
5y |
0 |
23y |
|||||||||
|
x |
6 |
7 |
8 |
9 |
|||||||||||
|
Шаг |
k |
d |
n |
k |
d |
n |
k |
d |
n |
k |
d |
n |
|||
|
0 |
0 |
x |
y |
0 |
x |
y |
0 |
x |
y |
0 |
x |
Y |
|||
|
1 |
0 |
3 |
2y |
y |
3 |
2y |
0 |
4 |
2y |
y |
4 |
2y |
|||
|
2 |
2y |
1 |
4y |
3y |
1 |
4y |
0 |
2 |
4y |
y |
2 |
4y |
|||
|
3 |
6y |
0 |
23y |
7y |
0 |
23y |
0 |
1 |
8y |
y |
1 |
8y |
|||
|
4 |
8y |
0 |
24y |
9y |
0 |
24y |
|||||||||
Примечание к таблице:
1) Шаг – шаг цикла
2) Шаг = 0 до цикла
Программная функция:
f = (x≠0, x – целое → k,n,d: = k+dn – 2n*(d div 2), d div 2, 2n)
k3 = k2 + d2n2 – 2n2*(d2 div 2) = k1 + d1n1 – 2n1*(d1 div 2) + (d1 div 2)*2n1 – 2*2n1*((d1 div 2) div 2) = k0 + d0n0 – 2n0*(d0 div 2) + (d0 div 2)*2n0 – 2*2*2*n0*((d1 div 2) div 2 div 2) = k0 + d0n0 – 23n0 * d0 div 23
|
x |
f(x) |
f(x0) |
|
k |
k + dn – 2n*(d div 2) |
0 |
|
n |
d div 2 |
x |
|
d |
2n |
Y |
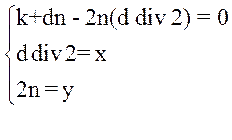
k + dn – xy = 0 – инвариант
1) Перед циклом
k=0 d=x n=y
k + dn – xy = 0
0 + xy – xy = 0
Предикат k + dn – xy = 0 – истинен
2) Во время исполнения цикла
k0 + d0n0 – 2n0(d0 div 2) + 2n0(d0 div 2) –xy = 0
0 + xy – xy = 0
3) После цикла
d=0 k=xy n=2my
k + dn – xy = xy + 0*2my – xy = 0
Ответ: k + dn – xy = 0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.