Обращение матрицы A размером N*N с помощью разложения в ряд при ОП компьютера: 2048 Mb (Лабораторная работа № 1)

Министерство образования и науки

Российской Федерации

НГТУ

Кафедра прикладной математики

Лабораторная работа №1

по “Архитектуре ЭВМ и вычислительных систем”

Факультет: ПМИ

Группа: ПМ-72

Студент: Щеголев В. С.

Преподаватель: Куликов И. М.

Новосибирск 2008

Задание

Обращение матрицы A размером N*N можно выполнить с помощью разложения в ряд:

где     ,   ,

, ,

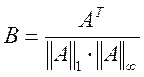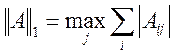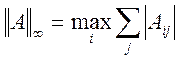I – единичная матрица (на диагонали – единицы, остальные – нули).

Тип данных float.

Размер N предполагается кратным четырем.

N=512,

Число шагов 10.

Ключ компиляции О2

Характеристика компьютера:

Процессор: Intel(R) Core(TM) 2 Duo processor T7300

(2.0 GHz, 800MHz FSB, 4 MB L2 cache)

ОП: 2048 MB

ОС: Microsoft Windows Vista

Текст программы:

#include <stdio.h>

#include <conio.h>

#include <time.h>

#include <stdlib.h>

#include <xmmintrin.h>

#include <math.h>

#define N 512

#define shag 10

float skal(float *x,float *y) // скалярное сложение векторов SSE

{ float sum; int i; __m128 *xx,*yy; __m128 p,s;

xx=(__m128 *)x;

yy=(__m128 *)y;

s=_mm_set_ps1(0);

for (i=0;i<N/4;i++)

{ p=_mm_mul_ps(xx[i], yy[i]); // векторное умножение четырех чисел

s=_mm_add_ps(s,p); // векторное сложение четырех чисел

}

p=_mm_movehl_ps(p,s); // перемещение двух старших значений s в младшие p

s=_mm_add_ps(s,p); // векторное сложение

p=_mm_shuffle_ps(s,s,1); //перемещение второго значения в s в младшую позицию в p

s=_mm_add_ss(s,p); // скалярное сложение

_mm_store_ss(&sum,s); // запись младшего значения в память

return sum;

}

void multiply(float A[],float B[],float C[]) // умножение матриц SSE

{ int i,j,k; float *mas;

mas = new float[N*N];

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) mas[j*N+i] = B[i*N+j];

for(i = 0;i<N;i++)

             for(j = 0;j<N;j++)

                       C[i*N+j] = skal(&A[i*N],&mas[j*N]);

}

void add(float A[],float B[],float C[]) // скалярное сложение матриц SSE

{ int i,j,k; __m128 p,s;

for(i=0;i<N;i++)

     { xx=(__m128*)&A[i*N];

yy=(__m128*)&B[i*N];

for(k = 0;k<N/4;k++)

{ p=_mm_add_ps(xx[k],yy[k]);

                      _mm_store_ps(&C[i*N+k*4],p);//запись четырех значений по выровненному адресу

}

     }  

}

void sub(float A[],float  B[],float C[])

{ int i,j,k; __m128 p;

for(i = 0;i<N;i++)

{ for(k = 0;k<N/4;k++)

{ __m128* xx,*yy;

xx=(__m128*)&A[i*N];

yy=(__m128*)&B[i*N];

p= _mm_sub_ps(xx[k],yy[k]);// векторное вычитание четырех чисел

_mm_store_ps(&C[i*N+k*4],p);

}

}

}

double S_SSE(float mas[],float TEK[]) // A^-1=(I+R+R²…)*B

{ float *I,*B,*R,*C,*pow,max_stolb,max_st; int sum,i,j; clock_t start1;

I = new float[N*N];

B = new float[N*N];

R = new float[N*N];

C = new float[N*N];

pow = new float[N*N];

max_stolb = 0;

sum = 0;

for(i = 0;i<N;i++) // макс сумма в столбце

{ for(j = 0;j<N;j++)

sum = sum + fabs(mas[i*N+j]);

if(sum>max1)

max_stolb = sum;

 }

max_st = 0;

sum = 0;

for(j = 0;j<N;j++)

{ for(i = 0;i<N;i++) // макс сумма в строке

sum = sum + fabs(mas[i*N+j]);

if(sum>max_st)

max_st = sum;

}

for(i = 0;i<N;i++)

for(j = i;j<N;j++)

{

B[(i)*N+(j)] =mas[(j)*N+(i)]/(max_stolb*max_st); // A^T=mas

}

for(i = 0;i<N;i++)

for(j=0;j<N;j++)

if(i==j) I[i*N+j] = 1; // единичная матрица

else I[i*N+j] = 0;

multiply(mas,B,C); // B*A=C

sub(I,C,R); // R=I-C

for(i = 0;i<N;i++)

for(j = 0;j<N;j++)

{ TEK[(i)*N+(j)] = I[i*N+j];

pow[i*N+j] = I[i*N+j];

}

start1 = clock();

for(int s = 1;s<=shag;s++)

{ multiply(pow,R,C); I*R=C

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) pow[i*N+j] = C[i*N+j];

add(TEK,pow,TEK); // TEK=(I+R+R²+…)

}

multiply(TEK,B,C); //C=TEK*B

start1 = clock() - start1;

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) TEK[i*N+j] = C[i*N+j]; // TEK=C

return (double)start1/(CLK_TCK*shag);

}

void umnoz(float A[],float B[],float C[])

{ int i,j,k;

for(i = 0;i<N;i++)

for(j=0;j<N;j++)

{ C[i*N+j]= 0;

for(k = 0;k<N;k++) C[i*N+j]+=A[i*N+k]*B[k*N+j];

}

}

void summa(float A[],float B[],float C[])

{ int i,j;

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) C[i*N+j]=A[i*N+j]+B[i*N+j];

 }

void razn(float A[],float B[],float C[])

{ int i,j;

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) C[i*N+j]=A[i*N+j]-B[i*N+j];

}

double normal(float mas[],float TEK[])

{ float *I,*B,*R,*C,*pow,max,maxst,sum; int i,j,s; clock_t start;

I = new float[N*N];

B = new float[N*N];

R = new float[N*N];

C = new float[N*N];

pow = new float[N*N];

max = 0;

sum = 0;

for(i = 0;i<N;i++)

{ for(j = 0;j<N;j++)

sum = sum + fabs(mas[i*N+j]);

if(sum>max) max = sum;

}

maxst = 0;

sum = 0;

for(j = 0;j<N;j++)

 { for(i = 0;i<N;i++)

sum = sum + fabs(mas[i*N+j]);

if(sum>maxst) maxst = sum;

}

for(i = 0;i<N;i++)

for(j = i;j<N;j++)

{

B[i*N+j] = mas[j*N+i]/(max*maxst);

}

for(i = 0;i<N;i++)

for(j=0;j<N;j++)

if(i==j) I[i*N+j] = 1;

else I[i*N+j] = 0;

umnoz(mas,B,C);

razn(I,C,R);

for(i = 0;i<N;i++)

for(j = 0;j<N;j++)

{ TEK[i*N+j] = I[i*N+j];

pow[i*N+j] = I[i*N+j];

}

start = clock();

for(s = 1;s<=shag;s++)

{ umnoz(pow,R,C);

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) pow[i*N+j] = C[i*N+j];

summa(TEK,pow,TEK);

}

umnoz(TEK,B,C);

start = clock() - start;

for(i = 0;i<N;i++)

for(j = 0;j<N;j++) TEK[i*N+j] = C[i*N+j];

return (double)start/(CLK_TCK*shag);

}

void main()

{ int i,j; double t,t1,t2; clock_t start; float *m1,*tech;

m1=new float[N*N];

tech=new float[N*N];

for(i=0;i<N;i++)

     for(j=0;j<N;j++) m1[i*N+j]= rand()/RAND_MAX*10;

start = clock(); // без SSE

t = normal(m1,tech);

start = clock() - start;

t1 =(double) start/CLK_TCK;

printf("Without: time of cicle %lf\n time out of cicle %lf",t,t1);

start = clock();// c SSE

t=S_SSE(m1,tech);

start = clock() - start;

t2 = start/CLK_TCK;

printf("\nWith: time of cicle %lf\n time out of cicle %lf",t,t2);

}

Результаты:

Без использования специальных расширений (обычный вариант):

Среднее время одной итерации цикла: 2.3558 с.;

Время вычислений вне цикла (общее время минус время в цикле): 25.127 с.

С использованием встроенных векторных функций расширения SSE.

Среднее время одной итерации цикла: 0.397 с.

Время вычислений вне цикла (общее время минус время в цикле): 4 с.