III. Несобственные интегралы.
Определение несобственного интеграла с бесконечным пределом:
Пусть f(x) определена
на [a;+ ∞) и интегрируема в любой конечной подобласти
этого промежутка. Предел этого интеграла (конечным или ∞) при b->∞
называется интегралом функции f(x)
от [a;∞) и обозначается (1)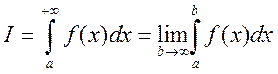 . В случае если, предел (1.1) конечен,
говорят, что интеграл (1) сходится, а f(x) тогда интегрируема на бесконечном промежутке [a;+∞). Если же lim(1)=∞ или не существует,
то интеграл расходится. Интеграл (1) – несобственный интеграл I рода
. В случае если, предел (1.1) конечен,
говорят, что интеграл (1) сходится, а f(x) тогда интегрируема на бесконечном промежутке [a;+∞). Если же lim(1)=∞ или не существует,
то интеграл расходится. Интеграл (1) – несобственный интеграл I рода
Свойства: Их сходимости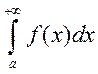 , 1)Сходится
, 1)Сходится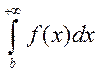 для всех b>a и наоборот. 2)
для всех b>a и наоборот. 2)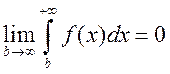 3) сходимость
3) сходимость 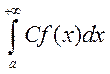 , С=const 4)Если сходится еще
, С=const 4)Если сходится еще 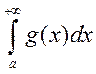 , то
сходится
, то
сходится 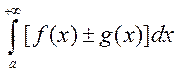
Признаки сходимости: Если f(x) положительна для любых x, то (4)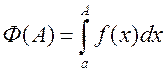 представляет собой монотонно возрастающую
функцию от А.
представляет собой монотонно возрастающую
функцию от А.
Т1. Для сходимости несобственного интеграла(1) в случае f(x)≥0 ó чтобы интеграл 4 оставался ограниченным сверху. Если это условие не выполняется, то интеграл имеет значение равное +∞.
Т2. Если при x≥A≥a имеет
место неравенство f(x)≤g(x), то из сходимости (5)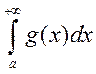 следует сходимость (6)
следует сходимость (6)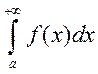 и наоборот для расходимости
и наоборот для расходимости
Т3. Если ![]() , то из сходимости
интеграла 5 вытекает сходимость 6 при k<∞, а из
расходимости 6 – сходимость 5 при k>0
, то из сходимости
интеграла 5 вытекает сходимость 6 при k<∞, а из
расходимости 6 – сходимость 5 при k>0
Признак Коши: Пусть для больших x f(x) представимо
в виде 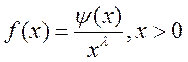 , Тогда,
, Тогда,
3) Если λ>1 и ψ(x)≤C≤+∞, то тогда интеграл 1 сходится
4) Если λ≤1 и ψ(x)≥C>0, то интеграл 1 расходится.
Т.е. для того, чтобы воспользоваться признаком Коши нужно определить, является ли f(x) при x-> 0 бесконечно малой порядка λ>0 по сравнению с 1/x;
Абсолютная сходимость: Если сходятся 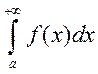 и (8)
и (8)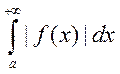 , то
интеграл 1 – абсолютно сходящийся., а f(x) – абсолютно интегрируема на [a;+∞)
, то
интеграл 1 – абсолютно сходящийся., а f(x) – абсолютно интегрируема на [a;+∞)
Если сходится 1, а 8 – расходится, то 1 – условно сходящийся.
Критерий Коши: Для сходимости интеграла 1 ó чтобы
для любых ε>0 существовало А0>a, что для любых А>А0 и А’>A0
выполнялось: 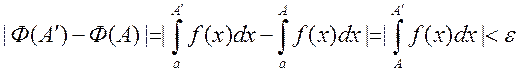 Следствие: Если сходится
интеграл с функцией по модулю, то сходится и интеграл с функцией без модуля.
Следствие: Если сходится
интеграл с функцией по модулю, то сходится и интеграл с функцией без модуля.
Признак Абеля: Пусть f(x) и g(x) определены на [a;+∞). Причем:
1)f(x)
интегрируема на этом промежутке так, что {интеграл вида 1} сходится хотя бы
неабсолютно. 2)g(x) монотонна
и ограничена на всем промежутке. |g(x)|≤L. Тогда интеграл 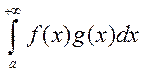 сходится.
сходится.
Доказательство: Пусть даны A`>A>a ->через теорему о среднем: на два интеграла до кси. Из условия 1 и вместо ε возьмем ε/2L, оценим и получим ≤ε;
Признак Дирихле:
1)f(x)
интегрируема в любом конечном промежутке [a;A] и интеграл от а до А ≤K; 2) g(x) монотонно ->0 при x->∞ и предел g(x)=0
при x->0., Тогда интеграл 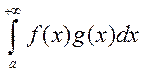 сходится.
сходится.
Доказательство: аналогично Абелю с учетом бесконечной малости g(x)
Определение несобственного интеграла от бесконечной функции(II Рода):
Пусть f(x) задана
на [a;b], но она не ограничена
в этом промежутке. Пусть f(x) ограничена
и интегрируема в любом конечном промежутке [a;b-η] где 0<η<b-a. f(x) не ограничена на [b-η;b]. Точка b называется особой точкой. Предел (1)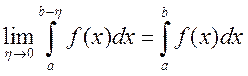 называется несобственным интегралом II Рода. Он может быть, как конечным,
так и бесконечным. Если конечен, то 1 – сходящийся интеграл, иначе –
расходящийся. Точка ∞ всегда является особой и требует дополнительного
предельного перехода.
называется несобственным интегралом II Рода. Он может быть, как конечным,
так и бесконечным. Если конечен, то 1 – сходящийся интеграл, иначе –
расходящийся. Точка ∞ всегда является особой и требует дополнительного
предельного перехода.
Теорема сравнения: Для сходимости несобственного интеграла 2 рода ó чтобы для любых η>0: интеграл 1 оставался ограниченным сверху.
Признак Коши:
Пусть для x достаточно близких к b-η f(x) может быть представлена в виде: f(x)=g(x)/(b-x)λ λ>0, тогда 1) λ<1 и g(x) ограничена верху, то 1-сходится, 2) λ≥1, а g(x) ограничена снизу, то расходится
Частный случай: x->b, f(x) – бесконечно большая по сравнению 1/b-x порядка λ. 1 сходится (расходится) при λ<1 (λ≥1)
Свойства несобственных интегралов второго рода:
|
1. |
5. f(x)≤g(x), то |
|
2. |
6. |
|
3. |
7. Существует |
|
4. |
8. Если при 7 в т. x=x0 f(x) непрерывна, то Ф’(x0)=f(x0) |
Теоремы о среднем:
Т1. Пусть f(x)
и g(x) интегрируемы на [a;b], причем f(x) ограничена, а g(x)
не меняет знака, тогда f(x)*g(x) будет интегрируема на [a;b] причем 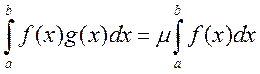
![]()
Т2. Пусть f(x)
монотонна и ограничена на [a;b],
а g(x) интегрируема на [a;b], Тогда f(x)*g(x) будет
интегрируема на [a;b]: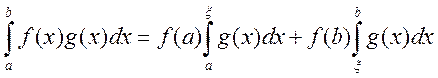
Интегрирование по частям:
Пусть u(x) и
v(x) определены и непрерывны
вместе со своими первыми производными в [a;b], кроме x=b(+∞),
тогда для 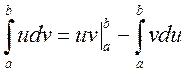
Замена переменных:
Пусть f(x)
определена и непрерывна в конечном или бесконечном [a;b] и интегрируема в этом интеграле в собственном смысле.
Рассмотрим монотонно возрастающую x=φ(t) непрерывную вместе со своей производной на [α;β], где β может быть ∞ и пусть φ(α)=a, φ(β)=b, тогда 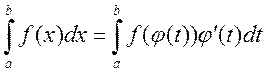
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.