Написание двух вариантов программы вычисления обратной матрицы (Лабораторная работы № 3)

МИНИСТЕРСТВО  НАУКИ И ОБРАЗОВАНИЯ РФ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ

Лабораторная работы № 3

По дисциплине

АРХИТЕКТУРА ЭВМ И СЕТЕЙ

Факультет: ПМИ

Студентка: Москаленко М.А.

Преподаватель: Дейкун М.В.

                            Маркова В.П.

Новосибирск 2006

Задание

Обращение матрицы A размером N*N можно выполнить с помощью разложения в ряд:

где     ,   ,

, ,

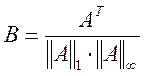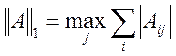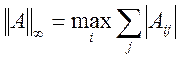I – единичная матрица (на диагонали – единицы, остальные – нули).

1)  Написать два варианта программы вычисления обратной матрицы:

-  без использования специальных расширений (обычный вариант),

-  с использованием встроенных векторных функций расширения SSE.

Каждый вариант программы:

-  оптимизировать по скорости, насколько это возможно,

-  проверить на правильность на небольшом тесте: (должно выполняться A^-1A=I).

Использовать тип данных float.

Размер N предполагать кратным четырем.

2)  Сравнить время работы двух вариантов программы для N=512, число шагов 10.

Определить:

-  среднее время одной итерации цикла (умножение + сложение матриц),

-  время вычислений вне цикла (общее время минус время в цикле).

Замер времени выполнить несколько раз, в качестве результата взять минимальное время. Для сравнения программы компилировать с наилучшей оптимизацией (нужно попробовать разнее комбинации ключи и выбрать лучшую).

#include <stdio.h>

#include <conio.h>

#include <math.h>

#include <time.h>

#include <xmmintrin.h>

#define N 512

#define Iter 10

void Transpanirovanie ( float Matrix [N*N], float Matrix1[N*N])

{

              float elem;

              int i,j;

              for(i=0;i<N;i++)

                            for(j=0;j<i+1;j++)

                            {

                                           elem = Matrix[i*N+j];

                                           Matrix1[i*N+j] = Matrix[j*N+i];

                                           Matrix1[j*N+i] = elem;

                            }

}

void Summ ( float Matrix[N*N], float Matrix1[N*N], float Matrix_Rezult[N*N])

{

              int i, k;

              __m128 *s,*p,*r;

              for(i=0;i<N;i++)

              {

                            for (k=0;k<N/4;k++)

                            {

                                           s=(__m128 *)&Matrix[i*N+4*k];

                                           p=(__m128 *)&Matrix1[i*N+4*k];

                                           r=(__m128 *)&Matrix_Rezult[i*N+4*k];

                                           *r=_mm_add_ps(*s,*p);          // векторное сложение четырех чисел

                            }

              }

}

void Umnozhenie ( float Matrix[N*N], float Matrix1[N*N], float Matrix_Rezult[N*N])

{

              int i,j,k;

  __m128 *xx,*yy;

  __m128 p,s;

              for(i=0;i<N;i++)

                            for(j=0;j<N;j++)

                            {

                                           xx=(__m128 *)&Matrix[i*N+0];

                                           yy=(__m128 *)&Matrix1[j*N+0];

                                           s=_mm_set_ps1(0);

                                           for (k=0;k<N/4;k++)

                                           {

                                                         _mm_prefetch((char *)&xx[k+4],_MM_HINT_NTA);

                                                         _mm_prefetch((char *)&yy[k+4],_MM_HINT_NTA);

                                           p=_mm_mul_ps(xx[k], yy[k]); // векторное умножение четырех чисел

                                                         s=_mm_add_ps(s,p);          // векторное сложение четырех чисел

                                           }

                                           p=_mm_movehl_ps(p,s); // перемещение двух старших значений s в младшие p

                                           s=_mm_add_ps(s,p);    // векторное сложение

                                           p=_mm_shuffle_ps(s,s,1); //перемещение второго значения в s в младшую                                                                               позицию в p

                                           s=_mm_add_ss(s,p);    // скалярное сложение

                                           _mm_store_ss(&Matrix_Rezult[i*N+j],s); // запись младшего значения в память

                            }

}

void Vichetanie ( float Matrix[N*N], float Matrix1[N*N], float Matrix_Rezult[N*N])

{

              int i, k;

              __m128 *s,*p,*r;

              for(i=0;i<N;i++)

              {

                            for (k=0;k<N/4;k++)

                            {

                                           s=(__m128 *)&Matrix[i*N+4*k];

                                           p=(__m128 *)&Matrix1[i*N+4*k];

                                           r=(__m128 *)&Matrix_Rezult[i*N+4*k];

                                           *r=_mm_sub_ps(*s,*p);          // векторное сложение четырех чисел

                            }

              }

}

float A1 ( float Matrix[N*N])

{

              float massiv[N], max=0;

              int i,j;

              for(i=0;i<N;i++)         massiv[i]=0;