Исследование частотно-манипулированных сигналов в средах micro-cap7.0 и matlab 6.5, страница 3

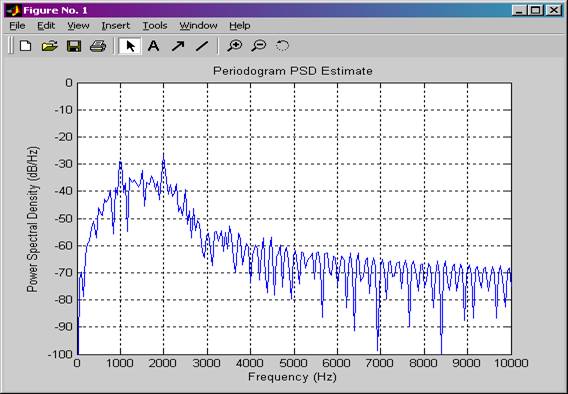
Рисунок 9. Спектр мощности ЧМн-сигнала для случая, когда манипулирующей функцией является ПСП 1.

Далее необходимо произвести построение АКФ ЧМн-сигнала. Для этого, в командной строке Matlab необходимо ввести:

>> K=length(td);

>> [tmp,R]=corrmtx(s_cpfsk,K-1);

>> plot(td,R(1,:))

Описание работы элемента программы:

·  В строке 1 определяется число элементов дискретного времени, для которого будет рассчитываться АКФ.

·  В строке 2 производится расчёт корреляционной матрицы ЧМн-сигнала.

·  Строка 3 выводит на экран первую строку этой матрицы, причём время для графика также отображается в символах. АКФ ЧМ-н сигнала, вычисленная таким способом, представлена на рисунке 10.

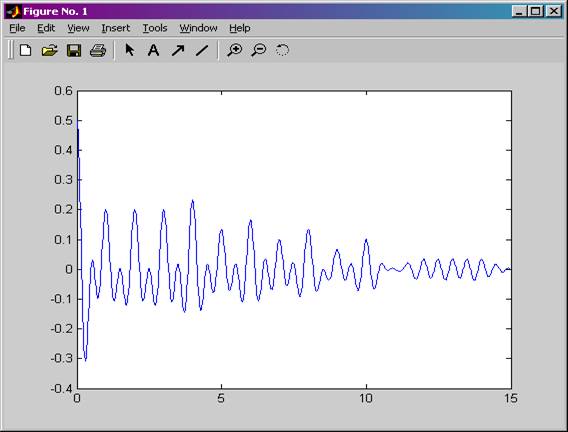
Рисунок 10. АКФ ЧМн-сигнала для случая, когда

манипулирующей функцией является ПСП 1.

Заключительным на данном этапе шагом является выполнение аналогичных действий при построении спектров и АКФ ЧМн-сигналов для двух оставшихся манипулирующих функций. Результаты проделанной работы приведены на рисунках ниже.

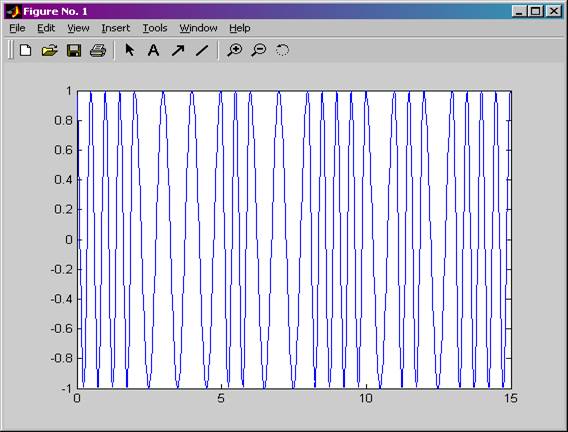
Рисунок 11. ЧМн сигнал во временной области для случая, когда манипулирующей функцией является ПСП 2.

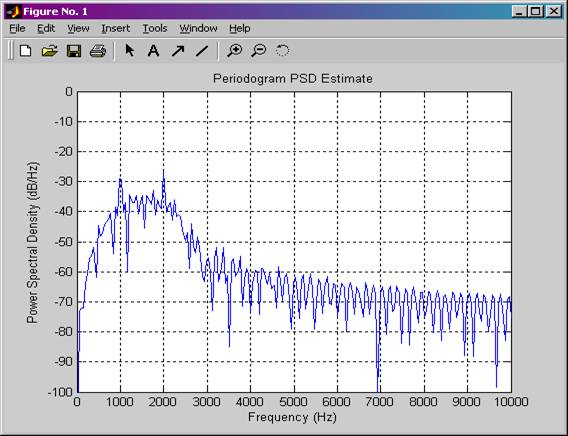
Рисунок 12. Спектр мощности ЧМн-сигнала для случая, когда манипулирующей функцией является ПСП 2.

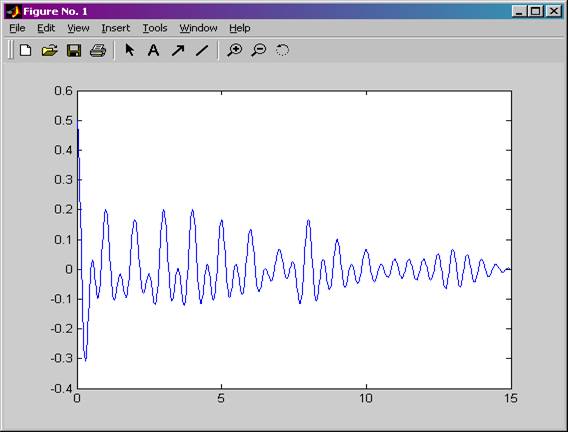
Рисунок 13. АКФ ЧМн-сигнала для случая, когда

манипулирующей функцией является ПСП 2.

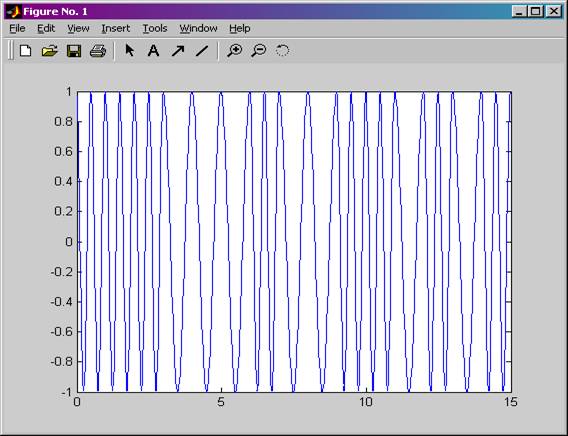
Рисунок 14. ЧМн сигнал во временной области для случая, когда манипулирующей функцией является ПСП 3.

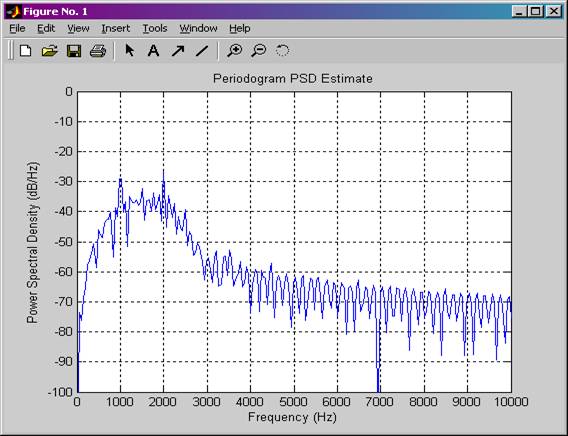
Рисунок 15. Спектр мощности ЧМн-сигнала для случая, когда манипулирующей функцией является ПСП 3.

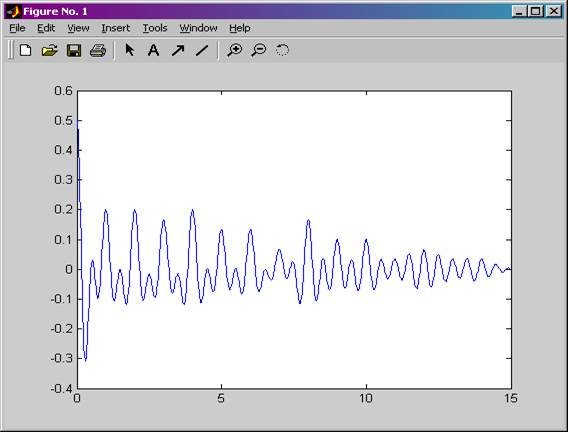
Рисунок 16. АКФ ЧМн-сигнала для случая, когда

манипулирующей функцией является ПСП 3.

Общие выводы о проделанной работе: в данной работе проводилось сравнение результатов моделирования в Micro-Cap 7.0 с результатами вычислений в среде Matlab 6.5. Интересен тот факт, что результаты, полученные в разных средах, являются  практически одинаковыми. Исключения составляют АКФ сигналов, построенные в Micro-Cap, так, как уже известно, что Micro-Cap выводит на экран только положительные значения АКФ сигналов.

Список литературы:

1.  Сергиенко А. Б. Цифровая обработка сигналов: Учебник для ВУЗов. – СПб.: Питер, 2002. – 608с.: ил.

2.  Дьяконов В. П. MATLAB 6/6.1/6.5 + Simulink 4/5 в математике и моделировании. Полное руководство пользователя. М.: СОЛОН-Пресс, 2003. – 576с.: ил.