Исследование частотно-манипулированных сигналов в средах micro-cap7.0 и matlab 6.5, страница 2

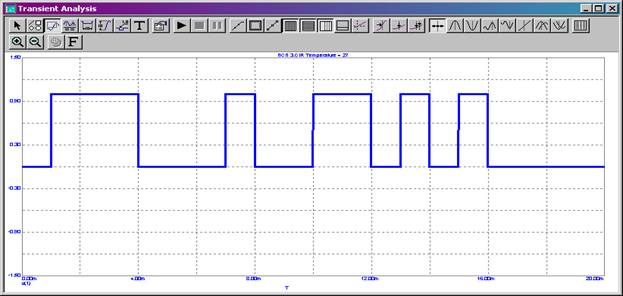
Рисунок 6. ПСП 3.

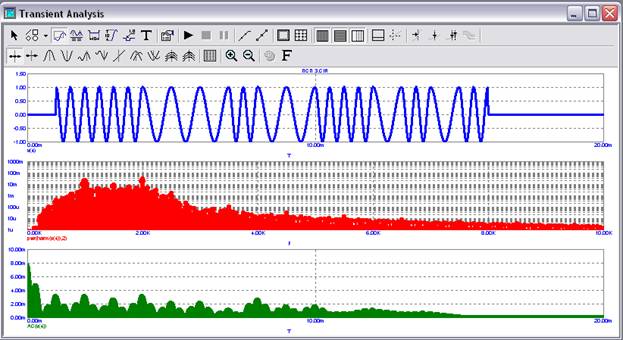
Рисунок 7. ЧМн-сигнал во временной области, его

спектральная плотность мощности  и АКФ для случая, когда манипулирующей функцией является ПСП 3.

Анализ спектров и АКФ ЧМн-сигналов в среде Matlab.

Ниже приведена программа для построения в Matlab сначала самого ЧМн-сигнала, а затем для расчёта его спектра и АКФ.

>> bits=[1 0 0 0 1 0 0 1 1 0 1 0 1 1 1];

>> N=length(bits);

>> Fd=1e3;

>> FsFd=50;

>> Fs=Fd*FsFd;

>> f=[1e3 2e3];

>> t=(0:FsFd-1)/Fs;

>> pps=2*pi*f/Fs;

>> s1=repmat(pps,FsFd,1);

>> d_cpfsk=s1(:,bits+1);

>> d_cpfsk=d_cpfsk(:);

>> phi_cpfsk=cumsum(d_cpfsk);

>> s_cpfsk=cos(phi_cpfsk);

>> td=(0:N*FsFd-1)/FsFd;

>> plot(td,s_cpfsk)

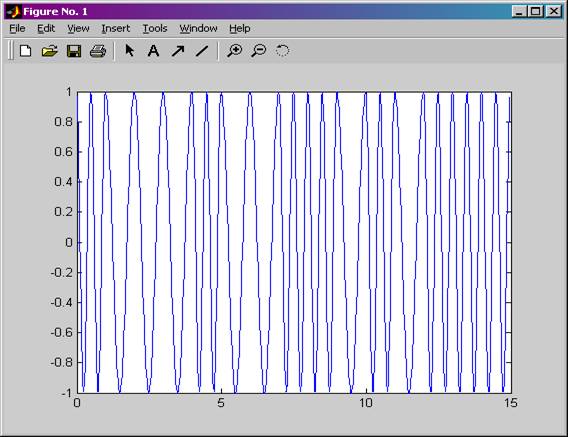
Рисунок 8. ЧМн сигнал во временной области для случая, когда манипулирующей функцией является ПСП 1.

Описание работы программы:

·  В первой строке задаётся цифровое сообщение (ПСП 1).

·  Во второй строке вычисляется длина сообщения (в битах).

·  Строка 3 задаёт скорость следования битов цифрового сообщения.

·  Строка 4 определяет количество отсчётов дискретного времени, приходящихся на один символ цифрового сообщения.

·  В строке 5 происходит вычисление частоты дискретизации.

·  В строке 6 задаются значения частот манипуляции.

·  В строке 7 определяется дискретное время для одного символа цифрового сообщения.

·  В строке 8 определяется сдвиг фазы на один отсчёт.

·  Строка 9 определяет фазовые сдвиги для 0 и 1 цифрового сообщения. Результатом действия функции repmat является матрица, содержащая два столбца, состоящие из FsFd элементов. В первом столбце будут содержаться значения фазовых сдвигов для 0, во втором – для 1.

·  В строке 10 происходит выбор столбца, соответствующего текущему символу сообщения. Итогом является формирование матрицы, содержащей 15 столбцов (15 бит цифрового сообщения) по FsFd элементов.

·  В строке 11 все столбцы матрицы, сформированной предыдущей строкой, выстраиваются подряд друг за другом. В результате получается матрица, состоящая из одного столбца, содержащая все необходимые фазовые сдвиги.

·  В строке 12 происходит интегрирование фазовых сдвигов для получения фазовой функции.

·  Строка 13 формирует ЧМн-сигнал.

·  Строка 14 организует время для графика в символах. Это сделано для удобства отображения.

·  Строка 15 выводит на экран график ЧМн-сигнала во временной области.

Такой способ формирования сигнала называется частотной манипуляцией с непрерывной фазовой функцией (continuous phase frequency shift keying, CPFSK). При этом формируется линейно меняющаяся полная фаза колебания, а передаваемые символы управляют скоростью её изменения. Или иначе: передаваемые символы переключают значение мгновенной частоты; эта частота интегрируется, давая непрерывную фазовую функцию; косинус такой полной фазы тоже будет непрерывной функцией.

Следующим шагом является построение спектра ЧМн-сигнала.

Для этого, в командной строке необходимо ввести следующее:

>> periodogram(s_cpfsk,[],[],Fs,'onesided')

Данная функция (периодограмма) является функцией непараметрического спектрального анализа. Вычисляет и выводит на экран график спектральной плотности мощности для одной (данной) реализации сигнала. При этом спектр ЧМ-н сигнала, вычисленный вышеуказанным способом представлен на рисунке 9.