Интегралы, зависящие от параметров
Рассмотрим ф-цию 2-х переменных f(x,y) которая
определена для ![]()
И пусть для ![]() ф-ция
f интегрируема
на отрезке [a,b] в собств.
Смысле (или несобств) Тогда
ф-ция
f интегрируема
на отрезке [a,b] в собств.
Смысле (или несобств) Тогда 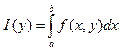 (1) будет ф-цией
параметра у.
(1) будет ф-цией
параметра у.
Если 1) для ф-ций F(x,y) при ![]()
![]() конечная предельная ф-я
конечная предельная ф-я
![]()
2) ![]()
то в этом случае можно сказать,
что ф-я f(x,y) стремится к
предельной ф-и ![]() равномерно отн-но Х
равномерно отн-но Х
ТЕОРЕМА 1: Если f(x,y) при
постоянном у интегрируема по х на [a,b] и при ![]() стремится к
стремится к ![]() равномерно
по Х, то имеет место равенство
равномерно
по Х, то имеет место равенство 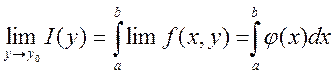
Д-ВО: Оценим 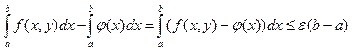 В
силу усл-я 2) из определения
В
силу усл-я 2) из определения
ТЕОРЕМА 2: Если ф-я f(x,y) опред и дифф как ф-я 2-х переменных на прямоугольнике [a,b;c,d]=[a,b]x[c,d] то интеграл (1) будет непрер ф-ей от у на [c,d].
Д-ВО: из определения равномерной непрерывности + Теорема 1
Правило Лейбница : Пусть сущ-ет
производная по у ф-и f(x,y) тогда
вычисление ![]() происходит след образом
происходит след образом 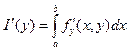 (5)
(5)
ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ ИНТЕГРАЛА
ТЕОРЕМА 3: Пусть f(x,y) опред в
прямоугольнике [a,b;c,d] и непрер по
х на [a,b] при ![]() постоянном у из [c,d]. Пусть во
всей области
постоянном у из [c,d]. Пусть во
всей области ![]() непрер как ф-я 2-х переменных.
непрер как ф-я 2-х переменных.
Тогда ![]() у
у![]() [c,d] имеет место
ф-ла (5)
[c,d] имеет место
ф-ла (5)
Д-ВО: Рассм. 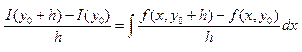 -
зависит от параметра h. Затем доказываем возможность предельного
перехода под знаком интеграла с помощью т.Лагранжа
-
зависит от параметра h. Затем доказываем возможность предельного
перехода под знаком интеграла с помощью т.Лагранжа
ИНТЕГРИРОВАНИЕ ПОД ЗНАКОМ ИНТЕГРАЛА
ТЕОРЕМА 4: Если ф-я f(x,y) - непрер
ф-я 2-х переменных в прямоугольнике [a,b;c,d] то имеет
место ф-ла 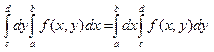
Д-ВО: доказываем вспомог. Рав-во 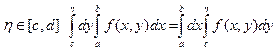 Вычисляем произв обеих частей рав-ва по
Вычисляем произв обеих частей рав-ва по ![]() и применяем к правой части правило
Лейбница. Получаем одно и тоже.
и применяем к правой части правило
Лейбница. Получаем одно и тоже.
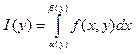 (8)
(8)
ТЕОРЕМА 5: Пусть f(x,y) опред и
непр в прямоугольнике [a,b;c,d], а кривые ![]() при
при ![]() непрер
и не выходят за пределы отрезков [c,d] и [a,b].
непрер
и не выходят за пределы отрезков [c,d] и [a,b].
Тогда 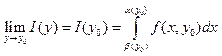 Д-ВО: (8)=
Д-ВО: (8)=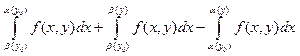 (9). Первый равен искомому
выражению, а остальные доказываем, что при
(9). Первый равен искомому
выражению, а остальные доказываем, что при![]() стремятся
к нулю.
стремятся
к нулю.
ТЕОРЕМА 6: Если кроме
условий теоремы 5 для ф-и f(x,y) выполняется
след - т.е. у нее ![]() произв по у т.е.
произв по у т.е. ![]() определ в [a,b;c,d] а у ф-и
определ в [a,b;c,d] а у ф-и ![]() и
и ![]() также
сущ произв
также
сущ произв ![]() ' и
' и![]() ’ тогда
интеграл (8) можно придифф по параметру у и эта производная будет равна
’ тогда
интеграл (8) можно придифф по параметру у и эта производная будет равна
(10) 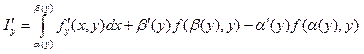
Д-ВО: воспользуемся соотношением
(9). 1-ый интеграл(пределы постоянны) по теор3 его производная равна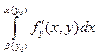 .Для второго и третьего по теореме о
среднем и переходя к пределу чтд.
.Для второго и третьего по теореме о
среднем и переходя к пределу чтд.
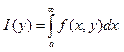 (1)
(1)
Условие
равномерной сходимости: Для того , чтобы интеграл (1) сх-ся равномерно от-но y
в области Y ![]()
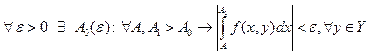
ПЕРВЫЙ ПРИЗНАК СХОДИМОСТИ
Пусть![]() интегрируема по х в каждом
конечном промежутке [a,b] если
интегрируема по х в каждом
конечном промежутке [a,b] если ![]() такая ф-я
такая ф-я ![]() интегрируемая в беск промежутке от А до +
интегрируемая в беск промежутке от А до +![]() что для любого
что для любого ![]() выполняется
след нер-во:
выполняется
след нер-во: ![]() то интеграл (1) сходится.
то интеграл (1) сходится.
Д-ВО: по св-вам мажоранты
ВТОРОЙ ПРИЗНАК СХОДИМОСТИ
Рассм.
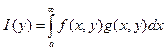 (3) .f(x,y)
интегр. По x
(3) .f(x,y)
интегр. По x![]() [a,b], a g(x,y) – монотонна по Х, если интеграл (1) сх-ся равн. От-но
у, а ф-я
[a,b], a g(x,y) – монотонна по Х, если интеграл (1) сх-ся равн. От-но
у, а ф-я ![]() < L равномерно
ограничена, то интеграл (3) сх-ся равномерно в области Y
< L равномерно
ограничена, то интеграл (3) сх-ся равномерно в области Y
ТРЕТИЙ ПРИЗНАК СХОДИМОСТИ
Если
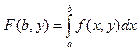 будет равном ограничен
будет равном ограничен 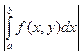
![]() , а ф-я g(x,y)
, а ф-я g(x,y)![]() при
при ![]() равномерно
отн-но у тогда интеграл (3) сх-ся равномерно от-но у
равномерно
отн-но у тогда интеграл (3) сх-ся равномерно от-но у
ЧЕТВЕРТЫЙ ПРИЗНАК СХОДИМОСТИ
(4)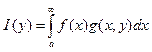 Если несобств интеграл
Если несобств интеграл 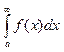 сх-ся, а g(x,y)
монотонна по х и равномерно ограничено, то интеграл (4) сх-ся равномерно.
сх-ся, а g(x,y)
монотонна по х и равномерно ограничено, то интеграл (4) сх-ся равномерно.
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ РАВН СХ-СТИ
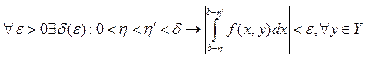
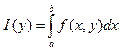 (1)
(1)
ТЕОРЕМА
1: пусть f(x,y) интегрируема в собств смысле на [![]() ] при
] при ![]() и в
каждом таком промежутке при
и в
каждом таком промежутке при ![]() f(x,y)
равномерно стремится к ф-и
f(x,y)
равномерно стремится к ф-и![]() . Если
. Если 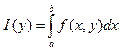 сх-ся равномерно при x=b, то
имеет место соотн-е
сх-ся равномерно при x=b, то
имеет место соотн-е 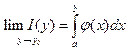
Д-ВО: по перестановке предельных переходов.
ТЕОРЕМА
2: Русть f(x,y) опред и дифф как ф-я 2-х переменных для ![]() y
y![]()
Если
интеграл (1) 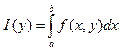 сх-ся равном, то этот интеграл
есть ф-я непрерыв на данном отрезке по у
сх-ся равном, то этот интеграл
есть ф-я непрерыв на данном отрезке по у
Д-ВО: аналог д-ву для собств интегралов
ТЕОРЕМА
3: Пусть выполнены условия теоремы 2 и ф-я f(x,y)
имеет непрер. По x и y производные, и пусть интеграл (1) сх-ся, а интеграл 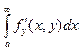 (3) сх-ся равномерно. Тогда
(3) сх-ся равномерно. Тогда ![]() имеет место
имеет место 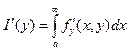
ТЕОРЕМА
4: При предположениях теоремы 2 тогда имеет место (4) 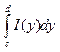
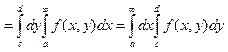
Д-ВО: основывается на определении равн сх-сти и на соотв теореме для собств интегралов.
ЭЙЛЕРОВЫ ИНТЕГРАЛЫ
Эйлеровым
интегралом 1 рода наз-ся интеграл вида 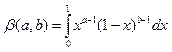 a,b>0
(1).
a,b>0
(1).
Он сх-ся для любых a,b>0 и опред след св-ва
1) ![]() док-во чеез подстановку x=1-t
док-во чеез подстановку x=1-t
2) ![]() док-во через интегр по частям и
развертывание рекурсии
док-во через интегр по частям и
развертывание рекурсии
3) 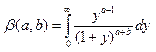 док-во через замену
док-во через замену ![]()
4) ![]()
Эйлеровым
интегралом 2 рода наз-ся интеграл вида(5)
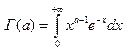 .
.
1)Г-функция
для " a>0 непрерывна и имеет непрерывную производную всех
порядков. (7)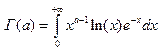 . 2)
. 2)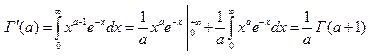 .
.
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.